Lösung von Aufgabe 9.3 S: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
[[Kategorie:Einführung_S]] | [[Kategorie:Einführung_S]] | ||
<br /> | <br /> | ||
| − | '''Idee:''' (Wir sind in einer Ebene E)<br /> | + | <br /><u>'''Idee:''' (Wir sind in einer Ebene E)<br /></u> |
Es gibt einen Punkt K, der nicht auf g liegt. Die Gerade s geht durch K und P. (Axiom I.1)<br /> | Es gibt einen Punkt K, der nicht auf g liegt. Die Gerade s geht durch K und P. (Axiom I.1)<br /> | ||
Also: g n s = {P}<br /> | Also: g n s = {P}<br /> | ||
Version vom 23. Juni 2012, 19:52 Uhr
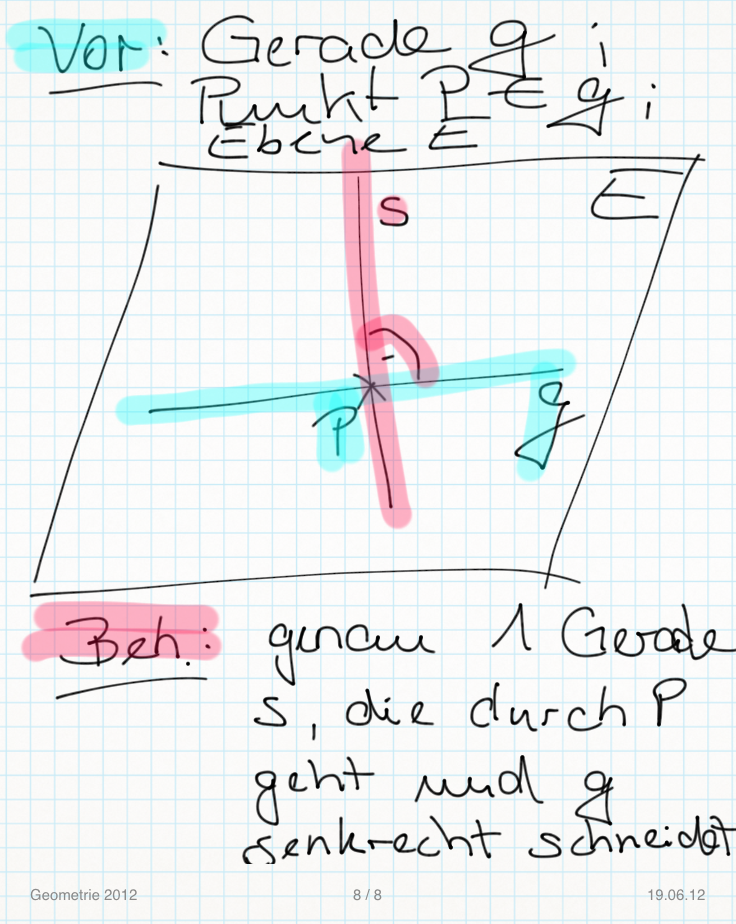
Satz:
Es sei 
eine Gerade der Ebene 
. Ferner sei 
ein Punkt auf . In der Ebene gibt es genau eine Gerade 
, die durch geht und senkrecht auf steht.
Beweisen Sie den Satz.
Lösungsversuch Nummero6/Tchu Tcha Tcha:
Eindeutigkeitsbeweis..Beweisen durch Widerspruch!
Annahme: Es gibt 2 nicht identische Geraden, die durch den Punkt P gehen und g senkrecht schneiden.
Fortsetzung folgt...
Könnte man hier nicht einen Widerspruchsbeweis mit dem Winkelkonstruktionsaxiom führen??
Letztendlich wird dann gesagt, dass es ein Widerspruch zu diesem Axiom wäre, da es nur genau einen Strahl in der Halbebene gibt, der das Maß 90 hat..?!?
die 2 Geraden müssten identisch sein, also Widerspruch zur Annahme! Behauptung stimmt..
--Tchu Tcha Tcha 16:56, 20. Jun. 2012 (CEST)
Idee: (Wir sind in einer Ebene E)
Es gibt einen Punkt K, der nicht auf g liegt. Die Gerade s geht durch K und P. (Axiom I.1)
Also: g n s = {P}
Winkel gPs hat das Maß 90 (Es gibt rechte Winnkel, Axiom W.4 --> Alle vier Winkel um P haben das Maß 90)
--> Eindeutigkeit und Existenz bewiesen. (!?)
--RitterSport 19:50, 23. Jun. 2012 (CEST)
