Lösung von Zusatzaufgabe 10.1P (SoSe 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 6: Zeile 6:
  
 
Zeichne einen Strahl <math>\ BA^{+}</math> . Zeichne einen weiteren, von <math>\ BA^{+}</math>  verschiedenen Strahl, <math>\ BC^{+}</math>  mit dem selben Anfangspunkt (Ursprung) wie <math>\ BA^{+}</math> . Zeichne einen Kreis k mit dem Mittelpunkt B und dem Radius <math>r=\left| \overline{BD}  \right|=\left| \overline{BE}  \right|, r>0 </math> . Zeichne nun einen Kreis p mit dem Mittelpunkt D und dem Radius von k. Zeichne nun einen Kreis l mit dem Mittelpunkt E und dem Radius von k. Zeichne den Punkt M an der Stelle mit der folgenden Bedingung ein: <math>\left\{ {M} \right\}= \ p \cap l \neq B</math>. Zeichne nun den Strahl <math>\ BM^{+}</math> . Zeichne die Strecke <math>\overline{DE}</math>  ein. Zeichne nun den Punkt P ein mit der folgenden Bedingung: <math>\left\{ {P} \right\} =\ \overline{DE}  \cap \ BM^{+} </math> .--[[Benutzer:Nolessonlearned|Nolessonlearned]] 16:08, 14. Jul. 2013 (CEST)<br />
 
Zeichne einen Strahl <math>\ BA^{+}</math> . Zeichne einen weiteren, von <math>\ BA^{+}</math>  verschiedenen Strahl, <math>\ BC^{+}</math>  mit dem selben Anfangspunkt (Ursprung) wie <math>\ BA^{+}</math> . Zeichne einen Kreis k mit dem Mittelpunkt B und dem Radius <math>r=\left| \overline{BD}  \right|=\left| \overline{BE}  \right|, r>0 </math> . Zeichne nun einen Kreis p mit dem Mittelpunkt D und dem Radius von k. Zeichne nun einen Kreis l mit dem Mittelpunkt E und dem Radius von k. Zeichne den Punkt M an der Stelle mit der folgenden Bedingung ein: <math>\left\{ {M} \right\}= \ p \cap l \neq B</math>. Zeichne nun den Strahl <math>\ BM^{+}</math> . Zeichne die Strecke <math>\overline{DE}</math>  ein. Zeichne nun den Punkt P ein mit der folgenden Bedingung: <math>\left\{ {P} \right\} =\ \overline{DE}  \cap \ BM^{+} </math> .--[[Benutzer:Nolessonlearned|Nolessonlearned]] 16:08, 14. Jul. 2013 (CEST)<br />
 +
* Deine Konstruktion ist sehr gut beschrieben und super nachvollziehbar - aber leider n'''icht die Lösung'''. Gegeben ist der Punkt P und der Winkel. Bei dir ist P das Endprodukt. --[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:37, 16. Jul. 2013 (CEST)
  
 
2) '''Beweis'''
 
2) '''Beweis'''

Version vom 16. Juli 2013, 11:37 Uhr

  1. Gegeben sei ein Winkel \angle ABC und ein Punkt P im Inneren des Winkels der nicht auf einem der Schenkel des Winkels \angle ABC liegt. Konstruieren Sie eine Strecke \overline{DE} deren Endpunkte D und E jeweils auf einem der beiden Schenkel des Winkels \angle ABC liegen und P Mittelpunkt der Strecke \overline{DE} ist.
  2. Beweisen Sie, dass Ihre Konstruktion richtig ist.

1) Konstruktion

Zeichne einen Strahl 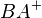\ BA^{+} . Zeichne einen weiteren, von 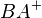\ BA^{+} verschiedenen Strahl, 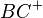\ BC^{+} mit dem selben Anfangspunkt (Ursprung) wie 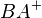\ BA^{+} . Zeichne einen Kreis k mit dem Mittelpunkt B und dem Radius 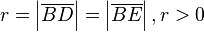r=\left| \overline{BD} \right|=\left| \overline{BE} \right|, r>0 . Zeichne nun einen Kreis p mit dem Mittelpunkt D und dem Radius von k. Zeichne nun einen Kreis l mit dem Mittelpunkt E und dem Radius von k. Zeichne den Punkt M an der Stelle mit der folgenden Bedingung ein: 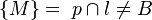\left\{ {M} \right\}= \ p \cap l \neq B. Zeichne nun den Strahl 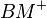\ BM^{+} . Zeichne die Strecke \overline{DE} ein. 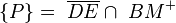Zeichne nun den Punkt P ein mit der folgenden Bedingung: \left\{ {P} \right\} =\ \overline{DE} \cap \ BM^{+} .--Nolessonlearned 16:08, 14. Jul. 2013 (CEST)

  • Deine Konstruktion ist sehr gut beschrieben und super nachvollziehbar - aber leider nicht die Lösung. Gegeben ist der Punkt P und der Winkel. Bei dir ist P das Endprodukt. --Tutorin Anne 11:37, 16. Jul. 2013 (CEST)

2) Beweis

Voraussetzung:
D͞E entspricht {D} = BC+ ∩ k und {E} = BA+ ∩ k
mit k ≔ {P | |PB| = |BD| = r, r > 0, r ∈ ℝ}

{M} = p ∩ l ≠ B
mit p,l ≔ {P | |PD| = |PE| = |BD| = r, r > 0, r ∈ ℝ}

{P} = D͞E ∩ BM+ und BM+ senkrecht D͞E
--Nolessonlearned 17:33, 14. Jul. 2013 (CEST)
Behauptung:
P ist Mittelpunkt von D͞E
--Nolessonlearned 17:33, 14. Jul. 2013 (CEST)

Beweisschritt Begründung
1) {P} = D͞E ∩ BM+ und BM+ senkrecht D͞E Voraussetzung, Konstruktion

Mittelsenkrechte

2) BD| = |BE| Voraussetzung;

Mittelsenkrechtenkriterium

3) DP| = |PE| (1); (2); Def. Mittelsenkrechte
4) P ist Mittelpunkt von D͞E (1); (3); Def. Mittelsenkrechte

--Nolessonlearned 17:33, 14. Jul. 2013 (CEST)
Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_10.1P_(SoSe_13)&oldid=24730“