Lösung von Zusatzaufgabe 10.1P (SoSe 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 52: Zeile 52:
 
| (1); (3); Def. Mittelsenkrechte
 
| (1); (3); Def. Mittelsenkrechte
 
|}<br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 17:33, 14. Jul. 2013 (CEST)
 
|}<br />--[[Benutzer:Nolessonlearned|Nolessonlearned]] 17:33, 14. Jul. 2013 (CEST)
 +
==Tipp für einen korrekten Beweis==
 +
1)
 +
Da D und E den selben Abstand von P haben müssen, können diese Punkte durch eine Punktspiegelung des Winkels an P gefunden werdene.
 +
2) Begründet werden kann die Konstruktion dann mit der Eigenschaft des Viereckes, dass ich durch den Winkel <ABC und dessen Spiegelbild erzeugt habe.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 20:59, 18. Jul. 2013 (CEST)

Version vom 18. Juli 2013, 20:59 Uhr

  1. Gegeben sei ein Winkel \angle ABC und ein Punkt P im Inneren des Winkels der nicht auf einem der Schenkel des Winkels \angle ABC liegt. Konstruieren Sie eine Strecke \overline{DE} deren Endpunkte D und E jeweils auf einem der beiden Schenkel des Winkels \angle ABC liegen und P Mittelpunkt der Strecke \overline{DE} ist.
  2. Beweisen Sie, dass Ihre Konstruktion richtig ist.

1) Konstruktion

Zeichne einen Strahl 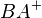\ BA^{+} . Zeichne einen weiteren, von 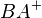\ BA^{+} verschiedenen Strahl, 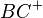\ BC^{+} mit dem selben Anfangspunkt (Ursprung) wie 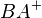\ BA^{+} . Zeichne einen Kreis k mit dem Mittelpunkt B und dem Radius 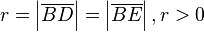r=\left| \overline{BD} \right|=\left| \overline{BE} \right|, r>0 . Zeichne nun einen Kreis p mit dem Mittelpunkt D und dem Radius von k. Zeichne nun einen Kreis l mit dem Mittelpunkt E und dem Radius von k. Zeichne den Punkt M an der Stelle mit der folgenden Bedingung ein: 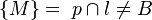\left\{ {M} \right\}= \ p \cap l \neq B. Zeichne nun den Strahl 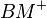\ BM^{+} . 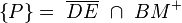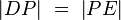Zeichne die Strecke \overline{DE} ein, mit der folgenden Bedingung: \left\{ {P} \right\} =\ \overline{DE}\ \cap \ BM^{+} und \left| DP \right| \ =\ \left| PE \right| .--Nolessonlearned 16:08, 14. Jul. 2013 (CEST)

  • Deine Konstruktion ist sehr gut beschrieben und super nachvollziehbar - aber leider nicht die Lösung. Gegeben ist der Punkt P und der Winkel. Bei dir ist P das Endprodukt. --Tutorin Anne 11:37, 16. Jul. 2013 (CEST)
    • Nun ist ist das Resultat die Strecke DE.--Nolessonlearned 17:09, 16. Jul. 2013 (CEST)


    • Das löst das Problem nicht, der Punkt P ist Voraussetzung und dieser liegt nicht unbedingt auf der Winkelhalbierenden. Gesucht ist die Strecke DE, wobei die Endpunkte nicht den selben Abstand von B haben müssen.--Tutorin Anne 07:36, 17. Jul. 2013 (CEST)
      • Dachte, da in der Aufgabenstellung steht, dass P in der Mitte der Strecke DE liegen muss, dass P ein Element der Winkelhalbierenden sein muss. Hast du einen Tipp für einen neuen Beweisansatz?--Nolessonlearned 07:07, 18. Jul. 2013 (CEST)

2) Beweis

  • Dein Beweis ist leider hinfällig, da die Konstruktion nicht der Aufgabenstellung entspricht.--Tutorin Anne 11:38, 16. Jul. 2013 (CEST)
    • Ich befürchte, dass ich eine falsche Voraussetzung gewählt habe.--Nolessonlearned 17:18, 16. Jul. 2013 (CEST)


Voraussetzung:
D͞E entspricht {D} = BC+ ∩ k und {E} = BA+ ∩ k
mit k ≔ {P | |PB| = |BD| = r, r > 0, r ∈ ℝ}

{M} = p ∩ l ≠ B
mit p,l ≔ {P | |PD| = |PE| = |BD| = r, r > 0, r ∈ ℝ}

{P} = D͞E ∩ BM+ und BM+ senkrecht D͞E
--Nolessonlearned 17:33, 14. Jul. 2013 (CEST)
Behauptung:
D͞E mit dem Mittelpunkt P
--Nolessonlearned 17:33, 14. Jul. 2013 (CEST)

Beweisschritt Begründung
1) {P} = D͞E ∩ BM+ und BM+ senkrecht D͞E Voraussetzung, Konstruktion

Mittelsenkrechte

2) BD| = |BE| Voraussetzung;

Mittelsenkrechtenkriterium

3) DP| = |PE| (1); (2); Def. Mittelsenkrechte
4) D͞E mit P als Mittelpunkt (1); (3); Def. Mittelsenkrechte

--Nolessonlearned 17:33, 14. Jul. 2013 (CEST)

Tipp für einen korrekten Beweis

1) Da D und E den selben Abstand von P haben müssen, können diese Punkte durch eine Punktspiegelung des Winkels an P gefunden werdene. 2) Begründet werden kann die Konstruktion dann mit der Eigenschaft des Viereckes, dass ich durch den Winkel <ABC und dessen Spiegelbild erzeugt habe.--Tutorin Anne 20:59, 18. Jul. 2013 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_10.1P_(SoSe_13)&oldid=24863“