Lösung von Zusatzaufgabe 5.1 (SoSe 12): Unterschied zwischen den Versionen
Nemo81 (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 1) |
||
| Zeile 3: | Zeile 3: | ||
<br /><br /> | <br /><br /> | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
| − | + | ==Lösung von Nemo81== | |
| + | ===Die Lösung=== | ||
Hier mal meine Lösung: | Hier mal meine Lösung: | ||
| Zeile 37: | Zeile 38: | ||
6) E1 geschnitten E2 = Gerdade g q.e.d --[[Benutzer:Nemo81|Nemo81]] 15:08, 30. Mai 2012 (CEST) | 6) E1 geschnitten E2 = Gerdade g q.e.d --[[Benutzer:Nemo81|Nemo81]] 15:08, 30. Mai 2012 (CEST) | ||
| + | ===Bemerkungen M.G.=== | ||
| + | Fall 1 muss nicht so "aufgebauscht" werden. Wir gehen von zwei Ebenen <math>E_1</math> und <math>E_2</math> aus. Es könnte sein, dass diese keinen Punkt gemeinsam haben: erster Teil der Behauptung. | ||
| + | |||
| + | Fall 2:<br /> | ||
| + | Es könnte auch sein, dass <math>E_1</math> und <math>E_2</math> (wenigstens) einen Punkt gemeinsam haben. In diesem Fall haben wir zu zeigen, dass der Schnitt von <math>E_1</math> mit <math>E_2</math> eine Gerade ist. | ||
| + | Sei <math>P</math> der Punkt, den <math>E_1</math> und <math>E_2</math> entsprechend unseres Falls gemeinsam haben. Axiom I/6 liefert uns jetzt einen weiteren Punkt <math>Q</math>, den die beiden Ebenen gemeinsam haben. Jetzt haben wir zwei Punkte, durch die genau die Gerade <math>PQ</math> geht. | ||
| + | |||
| + | Merken Sie, dass Ihr Schritt 2 nicht funktioniert? Sie gehen von zwei Tripeln von Punkten aus, durch die jeweils eine unserer beiden Ebenen geht. Wo kommen die auf einmal her diese Punkte? Und warum solen durch irgendwelche Punkte gerade unsere beiden Ebenen gehen. Sie machen hier denselben Fehler, wie bei der Lösung von Zusatzaufgabe 5.2. | ||
| + | |||
| + | Vergessen Sie Schritt zwei einfach. Sie hatten ja schon richtig erkannt, dass unsere Ebene im betrachteten Fall einen Punkt gemeinsam haben müssen. Beim Ihnen heißt dieser Punkt <math>C</math>. Sie wenden richtig das Axiom I/6 dann an, das Ihnen Ihren Punkt <math>P</math> liefert. Danach geht es korrekt mit I/1 und I/5 weiter. Merken Sie, dass Sie die vielen Punkte aus Ihrem Schritt 2 gar nicht brauchen? Also Schritt zwei anders formulieren: Entsprechend unserer Fallunterscheidung haben <math>E_1</math> und <math>E_2</math> einen Punkt gemeinsam. Danach läuft Ihr Beweis korrekt, bis wir bei Schritt 6 sind. Dieser ist so nicht korrekt. Wir wissen jetzt, dass Ihre Gerade <math>PC</math> zu <math>E_1</math> als auch zu <math>E_2</math> gehört, was sicherlich noch genauer zu begründen ist (I/5 dürfte helfen). Jetzt wissen wir nicht mehr und nicht weniger, als dass <math>PC</math> sowohl zu <math>E_1</math> als auch zu <math>E_2</math> gehört und damit zum Schnitt der beiden Ebene gehört. Wir wissen nicht, dass die Gerade <math>PC</math> die Schnittmenge der beiden Ebenen ist. Es bleibt also zu zeigen, dass unsere beiden Ebenen keine Punkt gemeinsam haben, der nicht auf <math>PC</math> liegt.--[[Benutzer:*m.g.*|*m.g.*]] 17:43, 3. Jun. 2012 (CEST) | ||
Version vom 3. Juni 2012, 17:43 Uhr
Inhaltsverzeichnis |
Aufgabe 1
Beweisen Sie Satz I.5 : Zwei voneinander verschiedene Ebenen haben entweder keinen Punkt oder eine Gerade gemeinsam, auf der alle gemeinsamen Punkte beider Ebenen liegen.
Lösung von Nemo81
Die Lösung
Hier mal meine Lösung:
Vor: E1 ungleich E2
Beh:E1 geschnitten E2 = ( ) oder E1 geschnitten E2= (Gerade g)
Direkter Beweis zwei Fälle
Fall 1:
1) E1 ungleich E2 laut Vor.
2) E1 parallel E2 laut Def I/10 (1)
3) E1 geschnitten E2 = ( ) q.e.d
Fall 2:
1) E1 ungleich E2 laut Vor.
2) Es existieren eine Ebene E1 für die gilt, A,B,C Element E1 und es existiert eine Ebene E2 für die gilt C,D,E element E2 laut Axiom I/4 und (1)
3) C ist Element E1 und C Element E2 laut (2)
4) es exist. ein Punkt P für den gilt P element E1 und P element E2 laut Axiom I/6
5) es exist. eine Gerade g für die gilt P ist element von g und C ist element von g laut Axiom I/1, (4), (3)
6) E1 geschnitten E2 = Gerdade g q.e.d --Nemo81 15:08, 30. Mai 2012 (CEST)
Bemerkungen M.G.
Fall 1 muss nicht so "aufgebauscht" werden. Wir gehen von zwei Ebenen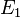 
und 
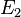aus. Es könnte sein, dass diese keinen Punkt gemeinsam haben: erster Teil der Behauptung.
Fall 2:
Es könnte auch sein, dass 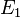und 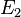(wenigstens) einen Punkt gemeinsam haben. In diesem Fall haben wir zu zeigen, dass der Schnitt von 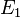mit 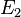eine Gerade ist.
Sei 
der Punkt, den 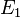und 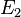entsprechend unseres Falls gemeinsam haben. Axiom I/6 liefert uns jetzt einen weiteren Punkt 
, den die beiden Ebenen gemeinsam haben. Jetzt haben wir zwei Punkte, durch die genau die Gerade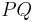 
geht.
Merken Sie, dass Ihr Schritt 2 nicht funktioniert? Sie gehen von zwei Tripeln von Punkten aus, durch die jeweils eine unserer beiden Ebenen geht. Wo kommen die auf einmal her diese Punkte? Und warum solen durch irgendwelche Punkte gerade unsere beiden Ebenen gehen. Sie machen hier denselben Fehler, wie bei der Lösung von Zusatzaufgabe 5.2.
Vergessen Sie Schritt zwei einfach. Sie hatten ja schon richtig erkannt, dass unsere Ebene im betrachteten Fall einen Punkt gemeinsam haben müssen. Beim Ihnen heißt dieser Punkt 
. Sie wenden richtig das Axiom I/6 dann an, das Ihnen Ihren Punkt liefert. Danach geht es korrekt mit I/1 und I/5 weiter. Merken Sie, dass Sie die vielen Punkte aus Ihrem Schritt 2 gar nicht brauchen? Also Schritt zwei anders formulieren: Entsprechend unserer Fallunterscheidung haben 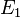und 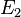einen Punkt gemeinsam. Danach läuft Ihr Beweis korrekt, bis wir bei Schritt 6 sind. Dieser ist so nicht korrekt. Wir wissen jetzt, dass Ihre Gerade 
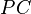zu 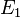als auch zu 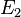gehört, was sicherlich noch genauer zu begründen ist (I/5 dürfte helfen). Jetzt wissen wir nicht mehr und nicht weniger, als dass 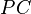sowohl zu 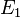als auch zu 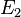gehört und damit zum Schnitt der beiden Ebene gehört. Wir wissen nicht, dass die Gerade 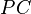die Schnittmenge der beiden Ebenen ist. Es bleibt also zu zeigen, dass unsere beiden Ebenen keine Punkt gemeinsam haben, der nicht auf 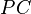liegt.--*m.g.* 17:43, 3. Jun. 2012 (CEST)
