Lösung von Zusatzaufgabe 6.2P (WS 12 13): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
Zeile 4: Zeile 4:
 
<br />
 
<br />
 
Beweis durch Kontraposition:<br />
 
Beweis durch Kontraposition:<br />
 +
Note: <math>\neg (Zw (A,B,C)\vee Zw (A,C,B)\vee Zw (B,A,C)) <=> \neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)</math><br />
 
{| class="wikitable"  
 
{| class="wikitable"  
−
| Voraussetzung || <math>\neg Zw (A,B,C) v \neg Zw (A,C,B) v \neg Zw (B,A,C)</math>
+
| Voraussetzung || <math>\neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)</math>
 
|-  
 
|-  
 
| Behauptung || <math>\neg koll (A,B,C)</math>
 
| Behauptung || <math>\neg koll (A,B,C)</math>

Version vom 19. Januar 2013, 16:36 Uhr

Beweisen Sie: Es sei \operatorname{koll} \left( A, B, C \right) mit \ A, B, C sind paarweise verschieden.
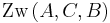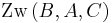Dann gilt genau eine der folgenden Zwischenrelationen: \operatorname{Zw} \left( A, B, C \right) oder \operatorname{Zw} \left( A, C, B \right) oder \operatorname{Zw} \left( B, A, C \right) .

Als Hilfe schon mal eine Tabelle. Für die Findung der Lösung darf auch nur angefangen werden. Ist es sinnvoll den Beweis direkt oder indirekt durch Widerspruch zu beweisen? Welche Definitionen sind vermutlich hilfreich? --Tutorin Anne 12:36, 10. Dez. 2012 (CET)

Beweis durch Kontraposition:
Note: 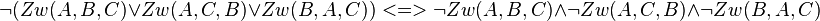\neg (Zw (A,B,C)\vee Zw (A,C,B)\vee Zw (B,A,C)) <=> \neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)

Voraussetzung 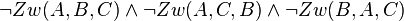\neg Zw (A,B,C) \wedge \neg Zw (A,C,B) \wedge \neg Zw (B,A,C)
Behauptung 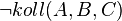\neg koll (A,B,C)


Fall 1: 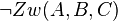\neg Zw (A,B,C) (Vor1)

Fall 2: 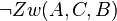\neg Zw (A,C,B) (Vor2)

Fall 3: 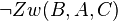\neg Zw (B,A,C) (Vor3)

Zu Fall 1:

Beweisschritt Begründung
1 |AB| + |BC| > |AC| v |AB| + |BC| < |AC| Vor1; Def. Zw
2 Es existiert ein Dreieck ABC 1.); Dreiecksungleichung
3 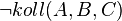\neg koll (A,B,C) 2.); Def. koll


Fall 2 und 3 analog zu Fall 1.
q.e.d.

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Zusatzaufgabe_6.2P_(WS_12_13)&oldid=20352“