Lösungen Serie 6 Einführung in die Geometrie SoSe 2020
Inhaltsverzeichnis |
Lösung Aufgabe 6.1
Aufgabe 6.1
Bestimmen Sie die folgenden Mengen:
-
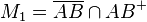 .
.
-
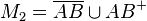 .
.
-
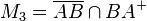 .
.
-
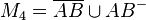 .
.
-
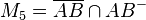 .
.
-
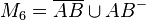 .
.
Lösung
Lösung Aufgabe 6.2
Aufgabe
Definieren Sie den Begriff Halbebene 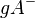 .
.
Lösung
Lösung Aufgabe 6.3
Aufgabe
Definition: (Dreieck)
- Es gelte
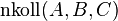 .
.
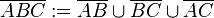 .
.
- Es gelte
Ergänzen Sie die Definition um den Begriff des Inneren des Dreiecks  .
.
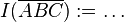 .
.
Lösung
Lösung Aufgabe 6.4
Aufgabe
Beweisen Sie den folgenden Satz:
Satz 6.1. (Schnitt konvexer Mengen)
- Die Schnittmenge zweier konvexer Mengen ist konvex.
Lösung
Es seien 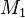 und
und  zwei konvexe Punktmengen ...
zwei konvexe Punktmengen ...
Lösung Aufgabe 6.5
Aufgabe
Beweisen Sie, dass jede Strecke  eine konvexe Menge ist.
eine konvexe Menge ist.
Lösung
Es seien  und
und  zwei Punkte der Strecke
zwei Punkte der Strecke  .
.
Wir haben zu zeigen, dass jeder Punkt von ....
Lösung Aufgabe 6.6
Aufgabe
Gegeben seien in der Ebene  die offene Halbebene
die offene Halbebene 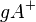 , die Trägergerade
, die Trägergerade  und die offene Halbebene
und die offene Halbebene 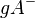 . Sie dürfen davon ausgehen, dass Folgendes bewiesen wurde:
. Sie dürfen davon ausgehen, dass Folgendes bewiesen wurde:
-
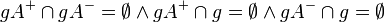 ,
,
-
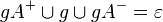 .
.
Satz 6.2 (Halbebenen sind konvex)
- Halbebenen sind konvexe Punktmengen.
Beweisen Sie Satz 6.2.
(Das Axiom von Pasch ist hilfreich)
Lösung
Wir beginnen mit der Halbebene 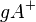 .
.
Es seien nun  und
und  zwei Punkte aus
zwei Punkte aus 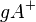 .
.
Wir haben zu zeigen, dass .....

