Lösungen Serie 8 Einführung in die Geometrie SoSe 2020: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(Die Seite wurde neu angelegt: „=Aufgabe 8.1= ==Aufgabe== Definieren Sie die Begriffe:<br /> :: a) Gleichschenkliges Dreieck, :: b) Schenkel eines gleichschenkligen Dreiecks, :: c) Basis ei…“)
 
(→‎Aufgabe 8.5)
 
(11 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 
=Aufgabe 8.1=
 
=Aufgabe 8.1=
 
==Aufgabe==
 
==Aufgabe==
−
Definieren Sie die Begriffe:<br />
+
Definieren Sie die Begriffe:
  
  
Zeile 10: Zeile 10:
  
 
==Lösung==
 
==Lösung==
−
::a) Ein Dreieck <math>\overline{ABC}</math> heißt gleichschnklig, wenn ...
+
::a) Ein Dreieck <math>\overline{ABC}</math> heißt gleichschenklig, wenn mindestens zwei Seiten kongruent sind.<br />
 +
::b) Die beiden Seiten eines gleichschenkligen Dreiecks, die kongruent zueinander sind, heißen Schenkel.<br />
 +
::c) Die Seite eines gleichschenkligen Dreiecks, die zu keiner anderen Seite kongruent ist, heißt Basis.
  
 +
=Aufgabe 8.2=
 +
[[Datei:Serie08Aufgabe8.2.jpg|thumb|Aufgabe 8.2]]
 +
==Aufgabe==
 +
Satz: Basiswinkel im gleichschenkligen Dreieck sind kongruent zueinander.
  
 +
::a) Formulieren Sie den Satz in "wenn...dann...Form".
 +
::b) Beweisen Sie den Satz, ohne den Kongruenzsatz SSS zu verwenden. Hinweis: Die Winkelhalbierende des Innenwinkels, der der Basis gegenüber liegt
 +
::Sollten Sie gar nicht zurechtkommen: http://geometrie.zum.de/images/3/31/Beweis_des_Basiswinkelsatzes.pdf
 +
==Lösung==
 +
 +
=Aufgabe 8.3=
 +
[[Datei:Serie08Aufgabe8.3.jpg|thumb|Aufgabe 8.3]]
 +
Definition: Mittelsenkrechte
 +
::Es seien $m$ eine Gerade und <math>\overline{AB}</math> eine Strecke mit dem Mittelpunkt <math>M</math>.
 +
Wenn <math>g \perp \overline{AB} \land M \in m</math>, dann heißt <math>m</math> Mittelsenkrechte von <math>\overline{AB}</math>
 +
 +
Beweisen Sie:
 +
:Satz: (Halbes Mittelsenkrechtenkriterium)
 +
::Es sei <math>m</math> die Mittelsenkrechte von <math>\overline{AB}</math>
 +
::<math>P \in m \Rightarrow \overline{PA} \cong \overline{PB}</math>
 +
 +
==Lösung==
 +
 +
=Aufgabe 8.4=
 +
[[Datei: Datei:20200702 203215.jpg thumb Serie 8 Aufgaben 3 und 4 |miniatur|[[Datei:20200702 203215.jpg|thumb|Serie 8 Aufgaben 3 und 4]]]]
 +
 +
=Aufgabe 8.5=
 +
[[Datei: Datei:20200702 203226.jpg thumb Serie 8 aufgabe 5 |miniatur|[[Datei:20200702 203226.jpg|thumb|Serie 8 aufgabe 5]]]]
 +
 +
=Aufgabe 8.6=
 +
 +
=Aufgabe 8.7=
 +
 +
=Aufgabe 8.8=
  
 +
=Aufgabe 8.9=
  
 +
=Aufgabe 8.10=
  
 
[[Kategorie: Einführung S]]
 
[[Kategorie: Einführung S]]

Aktuelle Version vom 2. Juli 2020, 20:38 Uhr

Inhaltsverzeichnis

Aufgabe 8.1

Aufgabe

Definieren Sie die Begriffe:


a) Gleichschenkliges Dreieck,
b) Schenkel eines gleichschenkligen Dreiecks,
c) Basis eines gleichschenkligen Dreiecks,
d) Basiswinkel eines gleichschenkligen Dreiecks,

Lösung

a) Ein Dreieck \overline{ABC} heißt gleichschenklig, wenn mindestens zwei Seiten kongruent sind.
b) Die beiden Seiten eines gleichschenkligen Dreiecks, die kongruent zueinander sind, heißen Schenkel.
c) Die Seite eines gleichschenkligen Dreiecks, die zu keiner anderen Seite kongruent ist, heißt Basis.

Aufgabe 8.2

Aufgabe 8.2

Aufgabe

Satz: Basiswinkel im gleichschenkligen Dreieck sind kongruent zueinander.

a) Formulieren Sie den Satz in "wenn...dann...Form".
b) Beweisen Sie den Satz, ohne den Kongruenzsatz SSS zu verwenden. Hinweis: Die Winkelhalbierende des Innenwinkels, der der Basis gegenüber liegt
Sollten Sie gar nicht zurechtkommen: http://geometrie.zum.de/images/3/31/Beweis_des_Basiswinkelsatzes.pdf

Lösung

Aufgabe 8.3

Aufgabe 8.3

Definition: Mittelsenkrechte

Es seien $m$ eine Gerade und \overline{AB} eine Strecke mit dem Mittelpunkt M.

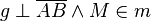Wenn g \perp \overline{AB} \land M \in m, dann heißt m Mittelsenkrechte von \overline{AB}

Beweisen Sie:

Satz: (Halbes Mittelsenkrechtenkriterium)
Es sei m die Mittelsenkrechte von \overline{AB}
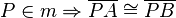
P \in m \Rightarrow \overline{PA} \cong \overline{PB}

Lösung

Aufgabe 8.4

Datei:Datei:20200702 203215.jpg thumb Serie 8 Aufgaben 3 und 4
Serie 8 Aufgaben 3 und 4

Aufgabe 8.5

Datei:Datei:20200702 203226.jpg thumb Serie 8 aufgabe 5
Serie 8 aufgabe 5

Aufgabe 8.6

Aufgabe 8.7

Aufgabe 8.8

Aufgabe 8.9

Aufgabe 8.10

Von „http://geometrie.zum.de/index.php?title=Lösungen_Serie_8_Einführung_in_die_Geometrie_SoSe_2020&oldid=35845“