Mittelsenkrechte, Mittelsenkrechtenkriterium und der Zusammenhang zur Geradenspiegelung WS 16 17: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=== Mittelsenkrechte === Eine Mittelsenkrechte ist das, was ihre Bezeichnung ausdrückt:eine Gerade, die eine Strecke halbiert und senkrecht auf ihr steht.<br …“) |
|||
| Zeile 1: | Zeile 1: | ||
=== Mittelsenkrechte === | === Mittelsenkrechte === | ||
Eine Mittelsenkrechte ist das, was ihre Bezeichnung ausdrückt:eine Gerade, die eine Strecke halbiert und senkrecht auf ihr steht.<br /> | Eine Mittelsenkrechte ist das, was ihre Bezeichnung ausdrückt:eine Gerade, die eine Strecke halbiert und senkrecht auf ihr steht.<br /> | ||
| − | Konstruieren Sie nachfolgend die Mittelsenkrechte:<br /> | + | Konstruieren Sie nachfolgend die Mittelsenkrechte:<br /> Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren].<br /><br /> |
<ggb_applet width="569" height="439" version="3.2" ggbBase64="UEsDBBQACAAIAEy90TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVZNU9swED2XX6HRHcd2CIWZGKalF2ZoOYRy6E2xN46KLLmSDAm/vquVnRho6bTTlovQ7no/3u5bZX6+aRS7B+uk0QXPkpQz0KWppK4L3vnV4Qk/PzuY12BqWFrBVsY2whd8muQ8yDt5dvBm7tbmgQlFJrcSHgq+EsoBZ661ICq3BvBP5KLbSCWF3V4vv0Lp3V4RnVzqtsMo3nYoK5vqSrrhOqGArZL+g7yXFVimTFnw4xmmjv/dgvWyFKrgR2mU5AXPnylRNA3atbHy0WgfzPfOVyhhzMlHwC/TIJtPqNA5dKWSlRQ6FEN5oBFjD7Ly64LPjk/RJch6HQA6Oo7eSmNstdg6Dw3bfAFr0Gk2C0Bv420abw7zwoCzlFTjG7mB+wV4j21xTGxgD1htZfXkcuneG7UXtUZqfyFa31nq6bQXLfw2BMBYNiT8TtcKelmGkK+hvFuazYJAyKbR9c22pU8ooWV9YZSxzAZ4Z2jQn8t4kk3IdGeVkk1KFr2P4HSnz05zsqBzGU+yUlLH1PrKs6HqLB3CSMeCIMCIo7grXoklYGs567T0V8MFR+BuX2r44FPXLJED4yHY+cz+ls/55Nn4zO/AalBxSDT2tjOdY/dhGGMsSqSCUjZ4jYqszy606zMmEKUV1BaGxCODImCkTceD+Ew8nwxJhBwc5lp6XAVYjw+1BKZ6ZEnBm6ROOKuED9JABQUNIE88zQSN1A6bd3y3FAzxe2Byr9+jjOofzgdNklDtWqBkoIASW2T7uCTyd71aOfBsU/DDHAm4xV0w0n401VMYhEY4qUakZBvch4a1AFW//3w/5azFgMSZUTcIRBeDJfkRhcsSPB/j12QUCRZWAwWe9t2PiP0Cu/f/Fbt/hk6evM0JHHwoTn4PndI0jdAV06LBSAuog5xQkeFVYCINE8ZEFsCKSHR+UIjorffxAmvXexvQFPzpgvFr5LEGh7TN97VOXm/JCICf9ST9846MJi5LTk4I1KPk9Dgd/WWE8GGWJdls9mJrvlIUfNPRxsXdJRt8WEvpd7iq0ONL7XGTAW2GlwvqDqANL8O1vrFCu/ALIdqMFt+uuZPxlqGHtf9lcfYdUEsHCKHQKG82AwAAiwgAAFBLAQIUABQACAAIAEy90Tyh0ChvNgMAAIsIAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAcAMAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" /> | <ggb_applet width="569" height="439" version="3.2" ggbBase64="UEsDBBQACAAIAEy90TwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1svVZNU9swED2XX6HRHcd2CIWZGKalF2ZoOYRy6E2xN46KLLmSDAm/vquVnRho6bTTlovQ7no/3u5bZX6+aRS7B+uk0QXPkpQz0KWppK4L3vnV4Qk/PzuY12BqWFrBVsY2whd8muQ8yDt5dvBm7tbmgQlFJrcSHgq+EsoBZ661ICq3BvBP5KLbSCWF3V4vv0Lp3V4RnVzqtsMo3nYoK5vqSrrhOqGArZL+g7yXFVimTFnw4xmmjv/dgvWyFKrgR2mU5AXPnylRNA3atbHy0WgfzPfOVyhhzMlHwC/TIJtPqNA5dKWSlRQ6FEN5oBFjD7Ly64LPjk/RJch6HQA6Oo7eSmNstdg6Dw3bfAFr0Gk2C0Bv420abw7zwoCzlFTjG7mB+wV4j21xTGxgD1htZfXkcuneG7UXtUZqfyFa31nq6bQXLfw2BMBYNiT8TtcKelmGkK+hvFuazYJAyKbR9c22pU8ooWV9YZSxzAZ4Z2jQn8t4kk3IdGeVkk1KFr2P4HSnz05zsqBzGU+yUlLH1PrKs6HqLB3CSMeCIMCIo7grXoklYGs567T0V8MFR+BuX2r44FPXLJED4yHY+cz+ls/55Nn4zO/AalBxSDT2tjOdY/dhGGMsSqSCUjZ4jYqszy606zMmEKUV1BaGxCODImCkTceD+Ew8nwxJhBwc5lp6XAVYjw+1BKZ6ZEnBm6ROOKuED9JABQUNIE88zQSN1A6bd3y3FAzxe2Byr9+jjOofzgdNklDtWqBkoIASW2T7uCTyd71aOfBsU/DDHAm4xV0w0n401VMYhEY4qUakZBvch4a1AFW//3w/5azFgMSZUTcIRBeDJfkRhcsSPB/j12QUCRZWAwWe9t2PiP0Cu/f/Fbt/hk6evM0JHHwoTn4PndI0jdAV06LBSAuog5xQkeFVYCINE8ZEFsCKSHR+UIjorffxAmvXexvQFPzpgvFr5LEGh7TN97VOXm/JCICf9ST9846MJi5LTk4I1KPk9Dgd/WWE8GGWJdls9mJrvlIUfNPRxsXdJRt8WEvpd7iq0ONL7XGTAW2GlwvqDqANL8O1vrFCu/ALIdqMFt+uuZPxlqGHtf9lcfYdUEsHCKHQKG82AwAAiwgAAFBLAQIUABQACAAIAEy90Tyh0ChvNgMAAIsIAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAcAMAAAAA" framePossible = "false" showResetIcon = "true" showAnimationButton = "true" enableRightClick = "true" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "true" showToolBarHelp = "true" showAlgebraInput = "true" allowRescaling = "true" /> | ||
| Zeile 16: | Zeile 16: | ||
=== Konstruktion eines Bildpunktes ''P''' bei der Spiegelung <math>S_{g}(P)</math> mit Zirkel und Lineal === | === Konstruktion eines Bildpunktes ''P''' bei der Spiegelung <math>S_{g}(P)</math> mit Zirkel und Lineal === | ||
| − | Nachfolgende GeoGebra-Applikation zeigt Schritt für Schritt die Vorgehensweise bei der Konstruktion des Bildpunktes ''P''' bei der Spiegelung <math>S_{g}(P)</math><br /><br /> | + | Nachfolgende GeoGebra-Applikation zeigt Schritt für Schritt die Vorgehensweise bei der Konstruktion des Bildpunktes ''P''' bei der Spiegelung <math>S_{g}(P)</math><br /><br />Falls nichts angezeigt wird, können Sie mit folgendem Link [{{fullurl:{{PAGENAME}}|action=purge}} den Servercache leeren].<br /><br /> |
<ggb_applet width="908" height="528" version="4.0" ggbBase64="UEsDBBQACAAIAO1YzkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAO1YzkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrrjts2Fv6dPgUhFP0V2+JVUmK38KQoNthJM9jJLopFgECWaJsZWXIk2eNJm//7Kvta+yR7SEq25Fs8t2IaJx5K5OHlfOc755CS+z+tZglayrxQWTpwcNd1kEyjLFbpZOAsynHHd3768bv+RGYTOcpDNM7yWVgOHKYlVTxwhEtGMYtYJxyLoMOwH3XCmONOEONxTIMIR9HYQWhVqBdp9ms4k8U8jORlNJWz8DyLwtJMPC3L+Yte7/r6ultP1c3ySW8yGXVXRewgWGZaDJzq4gUM1+p0TY04cV3c++3NuR2+o9KiDNNIOkirsFA/fvesf63SOLtG1youpwMnwMJBU6kmU9BJCOqgnhaaAyBzGZVqKQvo2rg1OpezuWPEwlS3P7NXKFmr46BYLVUs84HjdomPBQ+o7wsmiO8TB2W5kmlZyeJqzl49Wn+p5LUdVl+ZGZmDyixLRqEeEf3xByIucdFzXWBbECiEsE2urXOpLYgtmC24lWG2O7OizMowK8MAh6Uq1CiRA2ccJgUgqNJxDtZb3xflTSLNeqqKjfb4OehUqM8gTF2giYUc6l33uf4K+DLd0GsriRuzlvnilpPWUwauf/qU5F6K0npOwvfMSfgBNcWRSa3ep+iJeQNamMr8N9+dGekxNbdntPf3m1CwP0XFfq92lX7lHaiYatmKPaWcFdpfaIB4oGmPEQffEB6wnCMcQOERBN6AMEeMwy32kdClh6gHDQxR5CMthykyzsF9+MM8M5hAHAbTtR74JMIwEUOcImx8iiHwJGT8EnyUUJDgHHHopKfHRA9BBWIC7qiPGKxRu6SHQZBCR7iH6QmiGFHdGXuICCT0eJhpVxe+XjoMSZBwkcB6QPBq8GjrzSDvI6q1ERVcKp0vyhZE0SyuL8tsvrYFSEM82kQ9G59aQfFZPwlHMoE8caktidAyTLRHmInGWVqi2ojE1k3ycD5VUXEpyxJ6FehjuAzPw1KufgHpop7byEZZWlzkWfkqSxaztEAoyhJ3veYswY1rsl413NBGA2s28EaDaFx7e+fNoAUtCgnzZ3lRi4dx/FpLbEIDIPk2TW7OchlezTPVVqPfMymnLxdRomIVpv8CsupZNC5onYF0uKozkGZ2tZAsjy9vCmAwWv1b5hnEGB9ybvMDVr2xTYzsNhVRqJ2PBd2g+YHJbqom7rY7VbaTy7WFwpXcKDvJtWc3bl4XZ1myqTL6vwrn5SI3mwcIjrnWaphOEmk4YsItZOboapStLi05qB3r3c0c7irlRxODO8p1YOUgUJUjWxoZvbS1lGtkXCPh1mxT8bodB8RImHJkSyMF9LVLq1TFtZrYradRhYlorlP5TR2tNPl1ol+kqjyvb0oVXVWqYtvh18VsJNcUao+JH2rMfm+LY/0rmacyqSgNxlxki8J6aIPtsYzUDG5tQwVJqM31T1iArY3lJJf1whOzMbOAmdYWW3eqzVC/5Nnsdbp8B1zYWkC/V6+yX0S5mmvOoRGkgSu5YVWsihCySNzsp30QVI90tgB4Sg0NeOeinGa52XtBUIFSu14iZ7DTQqWhl2HoGuYLs4XTeKJs9BHi2jr12faNwaB5L9UMKcNkPg31Nq9SOglvZN6CwYz3Jou3wQHsjQbg5HNr27mUlhZ2vXAxh+GMN7WCFKBdoNXA6ZAug0x7A0vpukDtz3YHb7ewWlntZK3AbGu3LAX0sTh9BbHrXcTazP0rQOZ2hW8g41366Ih9+gYQgwOM5Zjb9cSDIBZls1mYxig128FziMHOZncSuppoKMQaPYvMoqwbJnaoaoAd8HU4X0M7ubd/u3cHfgMf6/IavsC6aAd3Pd/3G5l3JxuVsFG6gtNgYVJmWSVHc/E3FcfSbJJttv6U2i6FTRFqNk9UpMrjmL9SeZRso35hUac7qF99wMdxh4CsojWwWvxU6KFnrCxB9V6qEh49lF3ejseFLLUZhGuM0CHimNnuZAE1kekS1g07RYRWbvUU5ca1y0Of65oVNuFHt+Gq6jNueBN4aq5WaFjLD2upITEXlG5t5Ia0mmLIdAbQqWDITVaoGbXNDr1/V2Ow1VF2vE5L2F6ARlsE0YY1FJnsUGRoG86O86QdHIcPzxJ97pzYYmSL+zswmIx5TFDOmOcSgX2fGyqxLvEF91zucc4I8fxHzyZnp2eTx0ds41o2vOET4YR0wokIWICJSzzuizo6isCjnFLhB65HGX+Y5HxC2BseDnvkdmGP3JPQ413z1OcfG/g4vjuhn25oC7oc4pkQ2BXC84U+vLYi2z7/M3Fu1wPvEfT2cuPsMDfo7bhB78mNyQe8yw7NB304dtmd82KnOkB0MP1rsqfjQ+ILfEa5cKnrB8zbok9nX8Qx/NkTcx4la1LLoiqetHj0yjb9DAUxh1hY+W1y6Ku7HTAeJU+2DqOtJ0v80VPjz08HB9Il2Hd5wAR3XUwDr8IkEDQgNGDwCQR5jPT2RuV5lu/f1e9u2S5+COdZ8fI2bKu73C+UTR/xwHvYDP4jmqGN2SjLEhmmazxGBi/ouZA7j+AOo9gQeshzEPcCu10jwWEcT9dt/CR1E0c4crpuk+oc+1S08+0RFgf8IbSbPkXdyLHj+eHAdyknun5/5GvEuVb8U8cjX1GNWWuuvhL12m+R9oS9j4dg07u4h4t7sKsJWDPEEb86rgq+FQ/Nsyjc9TBhHP5RD/bhsJU8vOGjd38WZaBP9GPG9T4JANp9J3El5Vy/DHqbvsvDtNA/N7EyjXcdJzL845NkuMAneu9qngPomkXVyt7JVQlUgYaB88OnRVa+/HsuVYHev0To6gNG+mIxM8WF+TtTJTIX/whjtbCCeddWQYf//ee/k8H734fPz95/QXZAs4g2qiXM6rSX8CcCuEN0VZyH7+RvbU5UL5wLmavx5uWsecHoOjUbqwGKMszLC53RkXku2GXNJ7H6LYp5N+B7Ww/bNtuEr1uJHLQSaVppeMxKpxvka48dvg2DENx6j307g9CDBqFNg5w9jEG+dtb/FgzCuvw+BmEtg2jHgGgE1oB4VOXr919OB5x9Y4Bzdxdw2vVbeAf8dojzFuLfo/fZUuY6y/9+USH+BX1/OuT8qUNe/crsVMTJPsRJ641LQA8h3mv+IsH88Kf6DeuP/wdQSwcI1g6BliwJAABgKwAAUEsBAhQAFAAIAAgA7VjOQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACADtWM5A1g6BliwJAABgKwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMMJAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /><br /> | <ggb_applet width="908" height="528" version="4.0" ggbBase64="UEsDBBQACAAIAO1YzkAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAO1YzkAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vrrjts2Fv6dPgUhFP0V2+JVUmK38KQoNthJM9jJLopFgECWaJsZWXIk2eNJm//7Kvta+yR7SEq25Fs8t2IaJx5K5OHlfOc755CS+z+tZglayrxQWTpwcNd1kEyjLFbpZOAsynHHd3768bv+RGYTOcpDNM7yWVgOHKYlVTxwhEtGMYtYJxyLoMOwH3XCmONOEONxTIMIR9HYQWhVqBdp9ms4k8U8jORlNJWz8DyLwtJMPC3L+Yte7/r6ultP1c3ySW8yGXVXRewgWGZaDJzq4gUM1+p0TY04cV3c++3NuR2+o9KiDNNIOkirsFA/fvesf63SOLtG1youpwMnwMJBU6kmU9BJCOqgnhaaAyBzGZVqKQvo2rg1OpezuWPEwlS3P7NXKFmr46BYLVUs84HjdomPBQ+o7wsmiO8TB2W5kmlZyeJqzl49Wn+p5LUdVl+ZGZmDyixLRqEeEf3xByIucdFzXWBbECiEsE2urXOpLYgtmC24lWG2O7OizMowK8MAh6Uq1CiRA2ccJgUgqNJxDtZb3xflTSLNeqqKjfb4OehUqM8gTF2giYUc6l33uf4K+DLd0GsriRuzlvnilpPWUwauf/qU5F6K0npOwvfMSfgBNcWRSa3ep+iJeQNamMr8N9+dGekxNbdntPf3m1CwP0XFfq92lX7lHaiYatmKPaWcFdpfaIB4oGmPEQffEB6wnCMcQOERBN6AMEeMwy32kdClh6gHDQxR5CMthykyzsF9+MM8M5hAHAbTtR74JMIwEUOcImx8iiHwJGT8EnyUUJDgHHHopKfHRA9BBWIC7qiPGKxRu6SHQZBCR7iH6QmiGFHdGXuICCT0eJhpVxe+XjoMSZBwkcB6QPBq8GjrzSDvI6q1ERVcKp0vyhZE0SyuL8tsvrYFSEM82kQ9G59aQfFZPwlHMoE8caktidAyTLRHmInGWVqi2ojE1k3ycD5VUXEpyxJ6FehjuAzPw1KufgHpop7byEZZWlzkWfkqSxaztEAoyhJ3veYswY1rsl413NBGA2s28EaDaFx7e+fNoAUtCgnzZ3lRi4dx/FpLbEIDIPk2TW7OchlezTPVVqPfMymnLxdRomIVpv8CsupZNC5onYF0uKozkGZ2tZAsjy9vCmAwWv1b5hnEGB9ybvMDVr2xTYzsNhVRqJ2PBd2g+YHJbqom7rY7VbaTy7WFwpXcKDvJtWc3bl4XZ1myqTL6vwrn5SI3mwcIjrnWaphOEmk4YsItZOboapStLi05qB3r3c0c7irlRxODO8p1YOUgUJUjWxoZvbS1lGtkXCPh1mxT8bodB8RImHJkSyMF9LVLq1TFtZrYradRhYlorlP5TR2tNPl1ol+kqjyvb0oVXVWqYtvh18VsJNcUao+JH2rMfm+LY/0rmacyqSgNxlxki8J6aIPtsYzUDG5tQwVJqM31T1iArY3lJJf1whOzMbOAmdYWW3eqzVC/5Nnsdbp8B1zYWkC/V6+yX0S5mmvOoRGkgSu5YVWsihCySNzsp30QVI90tgB4Sg0NeOeinGa52XtBUIFSu14iZ7DTQqWhl2HoGuYLs4XTeKJs9BHi2jr12faNwaB5L9UMKcNkPg31Nq9SOglvZN6CwYz3Jou3wQHsjQbg5HNr27mUlhZ2vXAxh+GMN7WCFKBdoNXA6ZAug0x7A0vpukDtz3YHb7ewWlntZK3AbGu3LAX0sTh9BbHrXcTazP0rQOZ2hW8g41366Ih9+gYQgwOM5Zjb9cSDIBZls1mYxig128FziMHOZncSuppoKMQaPYvMoqwbJnaoaoAd8HU4X0M7ubd/u3cHfgMf6/IavsC6aAd3Pd/3G5l3JxuVsFG6gtNgYVJmWSVHc/E3FcfSbJJttv6U2i6FTRFqNk9UpMrjmL9SeZRso35hUac7qF99wMdxh4CsojWwWvxU6KFnrCxB9V6qEh49lF3ejseFLLUZhGuM0CHimNnuZAE1kekS1g07RYRWbvUU5ca1y0Of65oVNuFHt+Gq6jNueBN4aq5WaFjLD2upITEXlG5t5Ia0mmLIdAbQqWDITVaoGbXNDr1/V2Ow1VF2vE5L2F6ARlsE0YY1FJnsUGRoG86O86QdHIcPzxJ97pzYYmSL+zswmIx5TFDOmOcSgX2fGyqxLvEF91zucc4I8fxHzyZnp2eTx0ds41o2vOET4YR0wokIWICJSzzuizo6isCjnFLhB65HGX+Y5HxC2BseDnvkdmGP3JPQ413z1OcfG/g4vjuhn25oC7oc4pkQ2BXC84U+vLYi2z7/M3Fu1wPvEfT2cuPsMDfo7bhB78mNyQe8yw7NB304dtmd82KnOkB0MP1rsqfjQ+ILfEa5cKnrB8zbok9nX8Qx/NkTcx4la1LLoiqetHj0yjb9DAUxh1hY+W1y6Ku7HTAeJU+2DqOtJ0v80VPjz08HB9Il2Hd5wAR3XUwDr8IkEDQgNGDwCQR5jPT2RuV5lu/f1e9u2S5+COdZ8fI2bKu73C+UTR/xwHvYDP4jmqGN2SjLEhmmazxGBi/ouZA7j+AOo9gQeshzEPcCu10jwWEcT9dt/CR1E0c4crpuk+oc+1S08+0RFgf8IbSbPkXdyLHj+eHAdyknun5/5GvEuVb8U8cjX1GNWWuuvhL12m+R9oS9j4dg07u4h4t7sKsJWDPEEb86rgq+FQ/Nsyjc9TBhHP5RD/bhsJU8vOGjd38WZaBP9GPG9T4JANp9J3El5Vy/DHqbvsvDtNA/N7EyjXcdJzL845NkuMAneu9qngPomkXVyt7JVQlUgYaB88OnRVa+/HsuVYHev0To6gNG+mIxM8WF+TtTJTIX/whjtbCCeddWQYf//ee/k8H734fPz95/QXZAs4g2qiXM6rSX8CcCuEN0VZyH7+RvbU5UL5wLmavx5uWsecHoOjUbqwGKMszLC53RkXku2GXNJ7H6LYp5N+B7Ww/bNtuEr1uJHLQSaVppeMxKpxvka48dvg2DENx6j307g9CDBqFNg5w9jEG+dtb/FgzCuvw+BmEtg2jHgGgE1oB4VOXr919OB5x9Y4Bzdxdw2vVbeAf8dojzFuLfo/fZUuY6y/9+USH+BX1/OuT8qUNe/crsVMTJPsRJ641LQA8h3mv+IsH88Kf6DeuP/wdQSwcI1g6BliwJAABgKwAAUEsBAhQAFAAIAAgA7VjOQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACADtWM5A1g6BliwJAABgKwAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAMMJAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "false" /><br /><br /> | ||
Welche mathematischen Zusammenhänge zwischen den Punkten A,B,P und P' wurde für die Konstruktion genutzt?<br /> | Welche mathematischen Zusammenhänge zwischen den Punkten A,B,P und P' wurde für die Konstruktion genutzt?<br /> | ||
Aktuelle Version vom 6. Dezember 2016, 14:22 Uhr
Inhaltsverzeichnis |
Mittelsenkrechte
Eine Mittelsenkrechte ist das, was ihre Bezeichnung ausdrückt:eine Gerade, die eine Strecke halbiert und senkrecht auf ihr steht.
Konstruieren Sie nachfolgend die Mittelsenkrechte:
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
Definition VI.1: (Mittelsenkrechte)
- Es sei
 eine Gerade und
eine Gerade und  eine Strecke, die durch
eine Strecke, die durch  im Punkt
im Punkt  geschnitten wird.
geschnitten wird.  ist die Mittelsenkrechte von
ist die Mittelsenkrechte von  , wenn
, wenn
- Es sei
Zusammenhang Mittelsenkrechte und Geradenspiegelung
Es sei g eine Gerade und 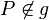 , ein beliebiger Punkt der mit g in der gleichen Ebene liegt. P' sei der Bildpunkt von P bei der Geradenspiegelung
, ein beliebiger Punkt der mit g in der gleichen Ebene liegt. P' sei der Bildpunkt von P bei der Geradenspiegelung 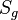 .
.
Nach der Definition Mittelsenkrechte und der Definition Geradenspiegelung ist die Spiegelgerade g Mittelsenkrechte der Strecke 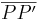 .
.
Konstruktion eines Bildpunktes P' bei der Spiegelung 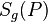 mit Zirkel und Lineal
mit Zirkel und Lineal
Nachfolgende GeoGebra-Applikation zeigt Schritt für Schritt die Vorgehensweise bei der Konstruktion des Bildpunktes P' bei der Spiegelung 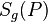
Falls nichts angezeigt wird, können Sie mit folgendem Link den Servercache leeren.
Welche mathematischen Zusammenhänge zwischen den Punkten A,B,P und P' wurde für die Konstruktion genutzt?
Ihre Antwort:
Wir können uns nun fragen: Ist der Punkt 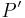 , den wir oben konstruiert haben, tatsächlich der Bildpunkt von P bei der Spiegelung
, den wir oben konstruiert haben, tatsächlich der Bildpunkt von P bei der Spiegelung 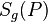 ?
?
Wenn wir beweisen könnten, dass  tatsächlich die Mittelsenkrechte der Strecke
tatsächlich die Mittelsenkrechte der Strecke 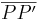 ist, dann wären wir fertig, denn dann wäre nach Definition Mittelsenkrechte und Geradenspiegelung, P' tatsächlich Bildpunkt von P bei der Spiegelung
ist, dann wären wir fertig, denn dann wäre nach Definition Mittelsenkrechte und Geradenspiegelung, P' tatsächlich Bildpunkt von P bei der Spiegelung 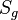 .
.
Nach unserer Konstruktion gilt: 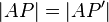 und
und 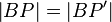 . Wir können also sagen, die beiden Punkte A und B haben zu den beiden Endpunkten der Strecke
. Wir können also sagen, die beiden Punkte A und B haben zu den beiden Endpunkten der Strecke 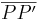 nach Konstruktion jeweils ein- und denselben Abstand. Außerdem gilt nach Konstruktion, dass A und B auf der Spiegelachse g liegen. Wenn wir nun beweisen könnten, dass alle und nur die Punkte, die auf der Mittelsenkrechten einer Strecke liegen zu den beiden Endpunkten dieser Strecke ein- und denselben Abstand haben, wüssten wir sicher, dass g die Mittelsenkrechte von
nach Konstruktion jeweils ein- und denselben Abstand. Außerdem gilt nach Konstruktion, dass A und B auf der Spiegelachse g liegen. Wenn wir nun beweisen könnten, dass alle und nur die Punkte, die auf der Mittelsenkrechten einer Strecke liegen zu den beiden Endpunkten dieser Strecke ein- und denselben Abstand haben, wüssten wir sicher, dass g die Mittelsenkrechte von 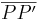 ist.
Genau das wollen wir jetzt beweisen. Wir gliedern dazu die obige Aussage in zwei Sätze:
ist.
Genau das wollen wir jetzt beweisen. Wir gliedern dazu die obige Aussage in zwei Sätze:
Satz VI.1 a: (hinreichende Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von 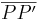 gehört.)
gehört.)
- Wenn ein Punkt
 zu den Endpunkten der Strecke
zu den Endpunkten der Strecke 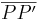 jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von
jeweils ein und denselben Abstand hat, so ist er ein Punkt der Mittelsenkrechten von 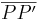 .
.
- Wenn ein Punkt
Satz VI.1 b (notwendige Bedingung dafür, dass ein Punkt zur Mittelsenkrechten von 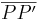 gehört)
gehört)
- Wenn ein Punkt
 zur Mittelsenkrechten der Strecke
zur Mittelsenkrechten der Strecke 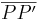 gehört, dann hat er zu den Punkten
gehört, dann hat er zu den Punkten  und
und  ein und denselben Abstand.
ein und denselben Abstand.
- Wenn ein Punkt
Beweisen werden wir die beiden Sätze in der Vorlesung bzw. in der Übung!
Wir können nun die beiden Sätze VI.1 a und VI.1 b zu einem neuen Satz zusammenfassen:
Satz VI.2: (Mittelsenkrechtenkriterium)
...