Probeklausur (SoSe 11): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→d) |
*m.g.* (Diskussion | Beiträge) (→e) |
||
| Zeile 40: | Zeile 40: | ||
Wir wissen bereits, dass Halbebenen konvexe Punktmengen sind. Begründen Sie, dass das Innere eines Winkels immer eine konvexe Punktmenge ist. Sie dürfen in Ihrer Begründung auf Sätze aus der Vorlesung verweisen, ohne diese noch einmal beweisen zu müssen. (Tabu ist diesbezüglich natürlich der Satz ''Das Innere eines Winkels ist konvex''.) | Wir wissen bereits, dass Halbebenen konvexe Punktmengen sind. Begründen Sie, dass das Innere eines Winkels immer eine konvexe Punktmenge ist. Sie dürfen in Ihrer Begründung auf Sätze aus der Vorlesung verweisen, ohne diese noch einmal beweisen zu müssen. (Tabu ist diesbezüglich natürlich der Satz ''Das Innere eines Winkels ist konvex''.) | ||
====e==== | ====e==== | ||
| − | Beweisen Sie: Jede Strecke | + | Beweisen Sie: Jede Strecke <math>\overline{AB}</math> hat höchstens einen Mittelpunkt. |
Version vom 26. Juni 2011, 17:08 Uhr
Inhaltsverzeichnis |
Die Klausur als PDF
Die Klausuraufgaben zum Diskutieren
Aufgabe 1
a
Definieren Sie den Begriff offene Strecke 
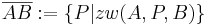
b
Definieren Sie, was man unter dem Kreis 
mit dem Radius 
und dem Mittelpunkt
versteht.
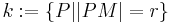
Der Kreis ist die Menge aller Punkte die zu den Abstand haben und mit in derselebn Ebene liegen. M heißt Mittelpunkt von k und r der Radius von k.
c
Definieren Sie den Begriff Inneres eines Kreises.
d
Was ist an der folgenden Definition nicht korrekt?
Definition (gleichschenkliges Dreieck):
- Wenn ein Dreieck zueinander kongruente Basiswinkel hat, so ist es gleichschenklig.
e
Unter dem Raum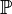 
versteht man die Menge aller Punkte. Die Punktmenge
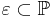sei eine Ebene. Gegeben sei ferner 
mit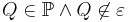 
. Definieren Sie die Begriffe Halbraum 
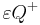und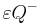 
.
f
Definieren Sie den Begriff regelmäßiges Sechseck. Der Begriff n-Eck sei bereits definiert.
Aufgabe 2
a
Es sei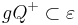 
eine offene Halbebene der Ebene 
. Es gelte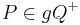
. Man beweise:
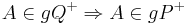. (Skizzen helfen)
b
Formulieren Sie die Kontraposition der Implikation aus Teilaufgabe a).
c
Warum bedarf die Implikation aus Teilaufgabe b) keines Beweises mehr?
d
Wir wissen bereits, dass Halbebenen konvexe Punktmengen sind. Begründen Sie, dass das Innere eines Winkels immer eine konvexe Punktmenge ist. Sie dürfen in Ihrer Begründung auf Sätze aus der Vorlesung verweisen, ohne diese noch einmal beweisen zu müssen. (Tabu ist diesbezüglich natürlich der Satz Das Innere eines Winkels ist konvex.)
e
Beweisen Sie: Jede Strecke hat höchstens einen Mittelpunkt.
