Reduktionssatz: Jede Bewegung ist die NAF von zwei oder drei Geradenspiegelungen
Inhaltsverzeichnis |
Drei nicht kollineare Punkte reichen aus
Satz:
- Jede Bewegung ist durch drei nicht kollineare Punkte und deren Bilder eindeutig bestimmt.
- Jede Bewegung ist durch drei nicht kollineare Punkte und deren Bilder eindeutig bestimmt.
Seien dies die Punkte A, B, C mit den Bildern A', B', C'.
Dazu nehmen wir an, dass es einen vierten Punkt D gibt, der zwei Bilder D' und D* mit D'  D*.
D*.
Der Beweis bietet sich in klassischer Tabellenform an.
| Schritt | Begründung |
|---|---|
1. 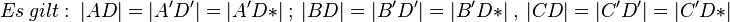 |
Annahme D hat zwei Punkte, Definition Bewegung |
2. Alle Punkte, für die gilt, dass sie von den Endpunkten einer Strecke je ein und denselben Abstand haben, ist die Mittelsenkrechte dieser Punkte. D. h. A', B' und C' liegen auf dieser Mittelsenkrechten von 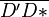 |
Definition Mittelsenkrechte, (1) |
| 3. Es gilt also: koll(A', B', C'). Da eine Gerade immer auf eine Gerade abgebildet wird, gilt auch koll(A, B, C) und das ist Widerspruch zur Voraussetzung - Annahme ist zu verwerfen. | (2), Geradentreue bei Bewegung, Definition kollinear |
--Flo60 18:20, 13. Mai 2012 (CEST)
Der Reduktionssatz
Satz: Reduktionssatz
- Jede Bewegung ist die Nacheinanderausführung von zwei oder drei Geradenspiegelungen.
Beweis
Es seien  drei nicht kollineare Punkte und
drei nicht kollineare Punkte und  eine Bewegung.
eine Bewegung.
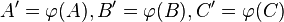 seien die Bilder von
seien die Bilder von  bei
bei 
Fall 1
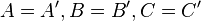
Fall 2
o.B.d.A.
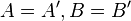
Wo muss C`liegen
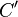 muss auf dem Kreis um
muss auf dem Kreis um  durch
durch  liegen.
liegen.
Begründung: Bewegungen sind abstandserhaltend.
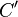 muss auf dem Kreis um
muss auf dem Kreis um  durch
durch  liegen.
liegen.
Begründung: Bewegungen sind abstandserhaltend.
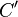 liegt damit in der Schnittmenge der beiden Kreise.
liegt damit in der Schnittmenge der beiden Kreise.
Warum wird  durch eine Spiegelung an
durch eine Spiegelung an  auf
auf 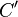 abgebildet?
abgebildet?
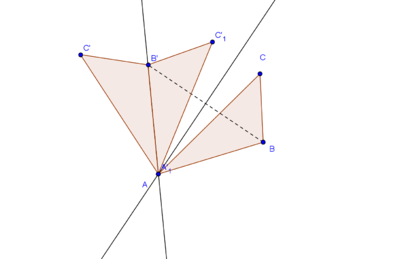
Es genügt zu zeigen, dass  die Mittelsenkrechte von
die Mittelsenkrechte von 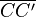 ist.
ist.
 ist die Mittelsenkrechte von
ist die Mittelsenkrechte von 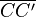 weil
weil
 und
und 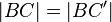 .
.
Fall 3
o.B.d.A.
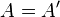
Spiegelung an der Mittelsenkrechten von 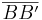 führt auf Fall 2 zurück.
führt auf Fall 2 zurück.
Fall 4
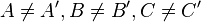
Fall 4.1
Umlaufsinn bleibt erhalten
Hier nochmal mit Bearbeitungsmöglichkeit (Einfügen von Mittelsenkrechten, Strecken etc.)
--Flo60 14:11, 29. Apr. 2012 (CEST)
Fall 4.2
Umlaufsinn bleibt nicht erhalten
--Flo60 14:11, 29. Apr. 2012 (CEST)