Serie 01
Aus Geometrie-Wiki
Version vom 19. Oktober 2011, 13:11 Uhr von Pipi Langsocke (Diskussion | Beiträge)
Inhaltsverzeichnis |
Aufgabe 1.1
- Definieren Sie für die ebene Geometrie den Begriff Bewegung
- (Definition 1.1)
Eine Bewegung ist eine Abbildung der Ebene auf sich, bei der Streckenlängen erhalten bleiben. Pipi Langsocke 12:45, 19. Okt. 2011 (CEST)
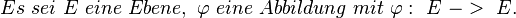
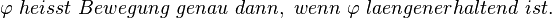
--Peterpummel 12:46, 19. Okt. 2011 (CEST)
Aufgabe 1.2
- Definieren Sie die Begriffe injektiv und surjektiv
injektiv: Es seien eine Ausgangsmenge M und eine Zielmenge N. Injektivität ist dann gegeben, wenn gilt: Jedes Element der Menge M kann einem Element der Zielmenge N eindeutig zugeordnet werden.
surjektiv: Es seien eine Ausgangsmenge M und eine Zielmenge N. Surjektivität ist dann gegeben, wenn gilt: Jedes Element der Zielmenge N besitzt mindestens ein Urbild in der Ausgangsmenge M. Pipi Langsocke 12:48, 19. Okt. 2011 (CEST)
Aufgabe 1.3
- Ergänzen Sie die folgende Tabelle
| Abbildung | Umkehrabbildung |
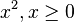 |
Wurzel(x) , x \ge 0 (Sorry für die Schreibweise!) -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST) |
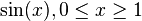 |
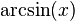 -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST) -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST)
|
Drehung um Z mit Drehwinkel  |
Drehung um Z mit dem Drehwinkel 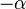 . -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST) . -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST)
|
Spiegelung an der Geraden  |
bleibt gleich -Pipi Langsocke 13:11, 19. Okt. 2011 (CEST) |
Aufgabe 1.4
- Beweisen Sie Satz 1.2
Es seien 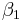 und
und 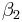 zwei Bewegungen.
zwei Bewegungen.
zu zeigen:
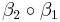 ist eine Bewegung.
ist eine Bewegung.

