Serie 01 12 13: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Aufgabe 01) |
(→zum Knobeln) |
||
| (2 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
=Aufgabe 02= | =Aufgabe 02= | ||
Gegeben seien die Punkte <math>A(5,3)</math> und <math>B(2,2)</math>. Bestimmen Sie die Gleichung der Geraden <math>AB</math> in der Form <math>y=mx+n</math>. | Gegeben seien die Punkte <math>A(5,3)</math> und <math>B(2,2)</math>. Bestimmen Sie die Gleichung der Geraden <math>AB</math> in der Form <math>y=mx+n</math>. | ||
| + | =Aufgabe 03= | ||
| + | Gegeben sie der Kreis <math>k</math> mit dem Mittelpunkt <math>M(x_M|y_M)</math> und dem Radius <math>r</math>. Entwickeln Sie eine Gleichung zur Beschreibung von <math>k</math>. | ||
=zum Knobeln= | =zum Knobeln= | ||
| Zeile 13: | Zeile 15: | ||
[[Bild:Schuetze.png|300px]]<br /> | [[Bild:Schuetze.png|300px]]<br /> | ||
<sup>Eingang Studentenklub Schützengasse</sup> | <sup>Eingang Studentenklub Schützengasse</sup> | ||
| + | |||
| + | <br /><br /> | ||
| + | =Lösung= | ||
| + | [[Lösungen zu den Aufgaben 1]] | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Aktuelle Version vom 17. Dezember 2012, 18:36 Uhr
Inhaltsverzeichnis |
Aufgabe 01
Gegeben sei ein Quader mit den Kantenlängen  ,
,  und
und  . Berechnen Sie die Länge der Raumdiagonale dieses Quaders.
. Berechnen Sie die Länge der Raumdiagonale dieses Quaders.
Aufgabe 02
Gegeben seien die Punkte 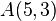 und
und 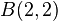 . Bestimmen Sie die Gleichung der Geraden
. Bestimmen Sie die Gleichung der Geraden  in der Form
in der Form 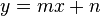 .
.
Aufgabe 03
Gegeben sie der Kreis  mit dem Mittelpunkt
mit dem Mittelpunkt 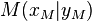 und dem Radius
und dem Radius  . Entwickeln Sie eine Gleichung zur Beschreibung von
. Entwickeln Sie eine Gleichung zur Beschreibung von  .
.
zum Knobeln
Die obige Grafik ist das Logo des Studentenklubs Schützengasse [1] der Bauhausuniversität Weimar. Dabei symbolisieren der kleinere innere Kreis den Kopf des Schützen, der große äußere Kreis zusammen mit der Spirale den Arm mit Bogen und schließlich das Bogendreieck die Pfeilspitze. Konstruieren Sie das Logo mit Geogebra.
Bemerkung: Leider hat die jüngere Generation von Studierenden das Logo ein wenig weiter entwickelt. Das ist zwar auch schön, mathematisch jedoch nicht mehr so ergiebig. Geblieben ist die alte Variante am Eingangsbereich des Klubs.

Eingang Studentenklub Schützengasse

