Serie 1 Gruppendefinition SoSe 2017: Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Aufgabe 1.2 Algebra SoSe 2016)
Zeile 11: Zeile 11:
 
Beweisen Sie: <math>\left[ M, \cdot \right ]</math> ist eine Gruppe.
 
Beweisen Sie: <math>\left[ M, \cdot \right ]</math> ist eine Gruppe.
  
−
=Aufgabe 1.2. Algebra SoSe 2017=
+
=Aufgabe 1.3. Algebra SoSe 2017=
 
Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.
 
Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.
 
# Geben Sie für jede der beiden Gruppen zwei Beispiele an.
 
# Geben Sie für jede der beiden Gruppen zwei Beispiele an.
−
# Definieren Sie was man unter der Klein'schen Vierergruppe  
+
# Definieren Sie was man unter der Klein'schen Vierergruppe versteht.
 +
# Definieren Sie die andere der beiden Vierergruppen.
 +
 
 +
=Aufgabe 1.4 Algebra SoSe 2017=
 +
Beweisen Sie: Bis auf Strukturgleichheit gibt es keine weitere Gruppe der Ordnung 4 als die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.
  
 
<!--- Was hier drunter steht muss stehen bleiben --->
 
<!--- Was hier drunter steht muss stehen bleiben --->

Version vom 7. Mai 2017, 18:12 Uhr

Inhaltsverzeichnis

Aufgabe 1.1 Algebra SoSe 2017

Formulieren Sie die Definition des Begriffs Gruppe unter Verwendung des Begriffs Halbgruppe.

Aufgabe 1.2 Algebra SoSe 2016

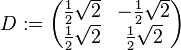D:=\begin{pmatrix} \frac{1}{2}\sqrt{2} & -\frac{1}{2}\sqrt{2} \\ \frac{1}{2}\sqrt{2} & \frac{1}{2}\sqrt{2} \end{pmatrix},
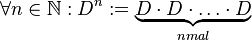\forall n \in \mathbb{N} : D^n := \underbrace{D \cdot D \cdot \ldots \cdot D}_{n mal},
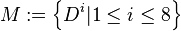M:=\left\{D^i|1 \leq i \leq 8 \right\} .
Beweisen Sie: \left[ M, \cdot \right ] ist eine Gruppe.

Aufgabe 1.3. Algebra SoSe 2017

Unter der Ordnung einer Gruppe versteht man die Anzahl ihrer Elemente. Es gibt (bis auf Isomorphie) genau 2 Gruppen der Ordnung 4. Die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.

  1. Geben Sie für jede der beiden Gruppen zwei Beispiele an.
  2. Definieren Sie was man unter der Klein'schen Vierergruppe versteht.
  3. Definieren Sie die andere der beiden Vierergruppen.

Aufgabe 1.4 Algebra SoSe 2017

Beweisen Sie: Bis auf Strukturgleichheit gibt es keine weitere Gruppe der Ordnung 4 als die Klein'sche Vierergruppe und die zyklische Gruppe der Ordnung 4.

Von „http://geometrie.zum.de/index.php?title=Serie_1_Gruppendefinition_SoSe_2017&oldid=29551“