Serie 2: Zwei Gleichungen mit zwei Unbekannten SoSe 2018: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.2 SoSe 2018) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 2.3 SoSe 2018) |
||
| Zeile 26: | Zeile 26: | ||
b) Generieren Sie für den potentiellen Fall der eindeutigen Lösbarkeit eine erweiterte Koeffizientenmatrix derart, dass das zugehörige Gleichungssystem wirklich eindeutig lösbar ist. Geben Sie diese Lösung an. | b) Generieren Sie für den potentiellen Fall der eindeutigen Lösbarkeit eine erweiterte Koeffizientenmatrix derart, dass das zugehörige Gleichungssystem wirklich eindeutig lösbar ist. Geben Sie diese Lösung an. | ||
=Aufgabe 2.3 SoSe 2018= | =Aufgabe 2.3 SoSe 2018= | ||
| − | Gegeben sei die Matrix <math>M=\begin{pmatrix} a & b \\ c & d \end{pmatrix}</math>. | + | Gegeben sei die Matrix <math>M=\begin{pmatrix} a & b \\ c & d \end{pmatrix}</math>. Die Determinante <math>M=\begin{vmatrix} a & b \\ c & d \end{vmatrix}</math> von <math>M</math> berechnet sich zu <math>a \cdot d - b \cdot c</math> |
| + | . Erläutern Sie den Zusammenhang zwischen drr Lösbarkeit eines LGS mit <math>M</math> als kleiner Koeffizientenmatrix und der Determinante von <math>M</math>. | ||
<!--- hier drunter nichts eintragen ---> | <!--- hier drunter nichts eintragen ---> | ||
[[Kategorie:Linalg]] | [[Kategorie:Linalg]] | ||
Version vom 3. Mai 2018, 17:00 Uhr
Aufgabe 2.1 SoSe 2018Gegeben Sei das Gleichungssystem Aufgabe 2.2 SoSe 2018Gegeben sind die kleinen Koeffizientenmatrizen:
a) In welchem Fall könnte das zugehörige Gleichungssystem eindeutig lösbar sein? Aufgabe 2.3 SoSe 2018Gegeben sei die Matrix |
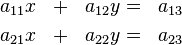 .
. 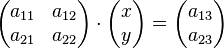 ist.
ist.
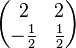

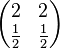
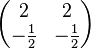
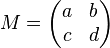 . Die Determinante
. Die Determinante 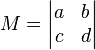 von
von  berechnet sich zu
berechnet sich zu 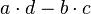 . Erläutern Sie den Zusammenhang zwischen drr Lösbarkeit eines LGS mit
. Erläutern Sie den Zusammenhang zwischen drr Lösbarkeit eines LGS mit 
