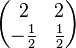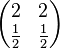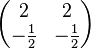Serie 2: Zwei Gleichungen mit zwei Unbekannten SoSe 2018

Aufgabe 2.1 SoSe 2018 Gegeben Sei das Gleichungssystem $\begin{align} && &a_{11}x &&+ &a_{12}y &= & a_{13} \\ && &a_{21}x &&+ &a_{22}y &= & a_{23} \end{align}$. Zeigen Sie, dass diese Schreibweise eines Gleichungssystems zur folgenden Schreibweise äquivalent ist: $\begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{pmatrix} \cdot \begin{pmatrix} x \\ y \end{pmatrix} =\begin{pmatrix} a_{13} \\ a_{23} \end{pmatrix}$ ist. Aufgabe 2.2 SoSe 2018 Gegeben sind die kleinen Koeffizientenmatrizen: $\begin{pmatrix} 2 & 2 \\ -\frac{1}{2} & \frac{1}{2} \end{pmatrix}$ $\begin{pmatrix} 2 & 2 \\ \frac{1}{2} & \frac{1}{2} \end{pmatrix}$ $\begin{pmatrix} 2 & 2 \\ -\frac{1}{2} & -\frac{1}{2} \end{pmatrix}$ a) In welchem Fall könnte das zugehörige Gleichungssystem eindeutig lösbar sein? 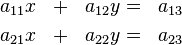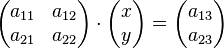b) Generieren sie für den potentiellen Fall der eindeutigen Lösbarkeit eine erweiterte Koeffizientenmatrix derart, dass das zugehörige Gleichungssystem wirklich eindeutig lösbar ist. Geben Sie diese Lösung an.