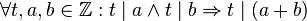Serie 2 SoSe 2018: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 3: | Zeile 3: | ||
'''Übungsaufgaben zum 04.05.2018'''<br /> | '''Übungsaufgaben zum 04.05.2018'''<br /> | ||
| − | Implikation, Voraussetzung, Behauptung, Umkehrung, Kontraposition, Widerspruchsbeweis | + | Implikation, Voraussetzung, Behauptung, Umkehrung, Kontraposition, Widerspruchsbeweis<br /> |
Hinweis: Für die geometrischen Beweise sind die Dreieckskongruenzsätze mitunter hilfreich. Sie finden sie hier: https://de.wikipedia.org/wiki/Kongruenzsatz | Hinweis: Für die geometrischen Beweise sind die Dreieckskongruenzsätze mitunter hilfreich. Sie finden sie hier: https://de.wikipedia.org/wiki/Kongruenzsatz | ||
| Zeile 24: | Zeile 24: | ||
Formulieren Sie den Basiswinkelsatz für Dreiecke in ''Wenn-Dann-Form'' und beweisen Sie ihn. Verwenden Sie für den Beweis die Existenz der Winkelhalbierenden eines Winkels und den Kongruenzsatz ''SWS''. Beziehen Sie sich in Ihrem Beweis sinnvollerweise auf eine Skizze. | Formulieren Sie den Basiswinkelsatz für Dreiecke in ''Wenn-Dann-Form'' und beweisen Sie ihn. Verwenden Sie für den Beweis die Existenz der Winkelhalbierenden eines Winkels und den Kongruenzsatz ''SWS''. Beziehen Sie sich in Ihrem Beweis sinnvollerweise auf eine Skizze. | ||
| − | =Aufgabe 2. | + | =Aufgabe 2.4 SoSe 2018= |
Eva formuliert die Umkehrung des Basiswinkelsatzes für Dreiecke wie folgt:<br /> | Eva formuliert die Umkehrung des Basiswinkelsatzes für Dreiecke wie folgt:<br /> | ||
:Wenn in einem Dreieck die Basiswinkel kongruent zueinander sind, dann ist das Dreieck gleichschenklig.<br /> | :Wenn in einem Dreieck die Basiswinkel kongruent zueinander sind, dann ist das Dreieck gleichschenklig.<br /> | ||
Warum ist Evas Formulierung nicht ganz korrekt? | Warum ist Evas Formulierung nicht ganz korrekt? | ||
| + | |||
| + | =Aufgabe 2.5 SoSe 2018= | ||
| + | Formulieren Sie den Innenwinkelsatz für Dreiecke in ''Wenn-Dann-Form''. | ||
| + | |||
| + | =Aufgabe 2.6 SoSe 2018= | ||
| + | Wir setzen den Innenwinkelsatz für Dreiecke und den Nebenwinkelsatz als bewiesen voraus.<br /> | ||
| + | '''Satz: (starker Außenwinkelsatz)''' | ||
| + | :Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden nicht anliegenden Innenwinkel. <br /> | ||
| + | a) Formulieren Sie den starken Außenwinkelatz in ''Wenn-Dann-Form''.<br /> | ||
| + | b) Formulieren Sie die Voraussetzung und die Behauptung des starken Außenwinkelsatzes unter Verwendung der Bezeichnungen in der folgenden Skizze:<br /> | ||
| + | |||
| + | |||
Version vom 28. April 2018, 11:51 Uhr
Übungsaufgaben zum 04.05.2018
Implikation, Voraussetzung, Behauptung, Umkehrung, Kontraposition, Widerspruchsbeweis
Hinweis: Für die geometrischen Beweise sind die Dreieckskongruenzsätze mitunter hilfreich. Sie finden sie hier: https://de.wikipedia.org/wiki/Kongruenzsatz
Inhaltsverzeichnis |
Aufgabe 2.1 SoSe 2018
Ein Blick über den Tellerrand der Geometrie:
Satz S:
a) Formulieren Sie Satz S schultauglich, d.h. weniger formal in einem normalen deutschen Satz.
b) Wie lautet die Voraussetzung in Satz S?
c) Wie lautet die Behauptung von Satz S.
d) Beweisen Sie Satz S.
Aufgabe 2.2 SoSe 2018
a) Bilden Sie sie Umkehrung von Satz S aus Aufgabe 2.1.
b) Begründen Sie: Die Umkehrung von Satz S ist keine wahre Aussage.
c) Formulieren Sie die Kontraposition von Satz S.
Aufgabe 2.3 SoSe 2018
Formulieren Sie den Basiswinkelsatz für Dreiecke in Wenn-Dann-Form und beweisen Sie ihn. Verwenden Sie für den Beweis die Existenz der Winkelhalbierenden eines Winkels und den Kongruenzsatz SWS. Beziehen Sie sich in Ihrem Beweis sinnvollerweise auf eine Skizze.
Aufgabe 2.4 SoSe 2018
Eva formuliert die Umkehrung des Basiswinkelsatzes für Dreiecke wie folgt:
- Wenn in einem Dreieck die Basiswinkel kongruent zueinander sind, dann ist das Dreieck gleichschenklig.
Warum ist Evas Formulierung nicht ganz korrekt?
Aufgabe 2.5 SoSe 2018
Formulieren Sie den Innenwinkelsatz für Dreiecke in Wenn-Dann-Form.
Aufgabe 2.6 SoSe 2018
Wir setzen den Innenwinkelsatz für Dreiecke und den Nebenwinkelsatz als bewiesen voraus.
Satz: (starker Außenwinkelsatz)
- Jeder Außenwinkel eines Dreiecks ist so groß wie die Summe der Größen der beiden nicht anliegenden Innenwinkel.
a) Formulieren Sie den starken Außenwinkelatz in Wenn-Dann-Form.
b) Formulieren Sie die Voraussetzung und die Behauptung des starken Außenwinkelsatzes unter Verwendung der Bezeichnungen in der folgenden Skizze: