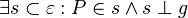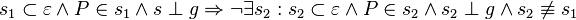Serie 9 SoSe 2013: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „=Definitionen= ==Aufgabe 9.1== Definieren Sie den Begriff Nebenwinkel. Lösung Aufgabe 9.1 WS_12_13 ==Aufgabe 9.2== Definieren Sie den Begriff Scheitelwinke…“) |
|||
| Zeile 1: | Zeile 1: | ||
=Definitionen= | =Definitionen= | ||
| − | ==Aufgabe 9. | + | ==Aufgabe 9.01== |
Definieren Sie den Begriff Nebenwinkel. | Definieren Sie den Begriff Nebenwinkel. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.01 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.02== |
Definieren Sie den Begriff Scheitelwinkel. | Definieren Sie den Begriff Scheitelwinkel. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.02 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.03== |
Definieren Sie den Begriff Außenwinkel eines Dreiecks <math>\overline{ABC}</math>. | Definieren Sie den Begriff Außenwinkel eines Dreiecks <math>\overline{ABC}</math>. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.03 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.04== |
Definieren Sie den Begriff Stufenwinkel. | Definieren Sie den Begriff Stufenwinkel. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.04 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.05== |
Definieren Sie den Begriff Wechselwinkel. | Definieren Sie den Begriff Wechselwinkel. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.05 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.06== |
Eine Winkelhalbierende ist ein Strahl. Ansonsten ist eine Winkelhalbierende das was ihr Name bereits semantisch verdeutlicht. | Eine Winkelhalbierende ist ein Strahl. Ansonsten ist eine Winkelhalbierende das was ihr Name bereits semantisch verdeutlicht. | ||
Definieren Sie den Begriff der Winkelhalbierenden eines Winkels <math>\angle ASB</math> | Definieren Sie den Begriff der Winkelhalbierenden eines Winkels <math>\angle ASB</math> | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.06 SS_13]] |
=Beweise= | =Beweise= | ||
| − | ==Aufgabe 9. | + | ==Aufgabe 9.07== |
In der Ebene <math>\varepsilon</math> seien eine Gerade <math>g</math> und ein Punkt <math>P</math> mit <math>P \in g</math> gegeben.<br /> | In der Ebene <math>\varepsilon</math> seien eine Gerade <math>g</math> und ein Punkt <math>P</math> mit <math>P \in g</math> gegeben.<br /> | ||
Beweisen Sie:<br /> | Beweisen Sie:<br /> | ||
| Zeile 41: | Zeile 41: | ||
#<math>s_1 \subset \varepsilon \wedge P \in s_1 \wedge s \perp g \Rightarrow \neg \exist s_2: s_2 \subset \varepsilon \wedge P \in s_2 \wedge s_2 \perp g \wedge s_2 \not \equiv s_1 </math> | #<math>s_1 \subset \varepsilon \wedge P \in s_1 \wedge s \perp g \Rightarrow \neg \exist s_2: s_2 \subset \varepsilon \wedge P \in s_2 \wedge s_2 \perp g \wedge s_2 \not \equiv s_1 </math> | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.07 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.08== |
Formulieren Sie die Aussagen 1 und 2 aus der vorangegangenen Aufgabe 9.7 als einen einzigen Satz kurz und prägenant derart, dass auch Schüler der SI diesen Satz verstehen können. | Formulieren Sie die Aussagen 1 und 2 aus der vorangegangenen Aufgabe 9.7 als einen einzigen Satz kurz und prägenant derart, dass auch Schüler der SI diesen Satz verstehen können. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.08 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.09== |
Beweisen Sie:<br /> | Beweisen Sie:<br /> | ||
::Wenn <math>P</math> im Inneren des Winkels <math>\angle ASB</math> liegt, dann ist <math>\left|\angle ASP \right| \le \left| \angle ASB \right|</math>. | ::Wenn <math>P</math> im Inneren des Winkels <math>\angle ASB</math> liegt, dann ist <math>\left|\angle ASP \right| \le \left| \angle ASB \right|</math>. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.09 SS_13]] |
| − | ==Aufgabe 9. | + | ==Aufgabe 9.010== |
Beweisen Sie:<br /> | Beweisen Sie:<br /> | ||
::Jeder Winkel hat genau eine Winkelhalbierende. | ::Jeder Winkel hat genau eine Winkelhalbierende. | ||
| − | [[Lösung Aufgabe 9. | + | [[Lösung Aufgabe 9.010 SS_13]] |
Version vom 18. Juni 2013, 09:50 Uhr
Inhaltsverzeichnis |
Definitionen
Aufgabe 9.01
Definieren Sie den Begriff Nebenwinkel.
Aufgabe 9.02
Definieren Sie den Begriff Scheitelwinkel.
Aufgabe 9.03
Definieren Sie den Begriff Außenwinkel eines Dreiecks 
.
Aufgabe 9.04
Definieren Sie den Begriff Stufenwinkel.
Aufgabe 9.05
Definieren Sie den Begriff Wechselwinkel.
Aufgabe 9.06
Eine Winkelhalbierende ist ein Strahl. Ansonsten ist eine Winkelhalbierende das was ihr Name bereits semantisch verdeutlicht.
Definieren Sie den Begriff der Winkelhalbierenden eines Winkels 
Beweise
Aufgabe 9.07
In der Ebene 
seien eine Gerade 
und ein Punkt 
mit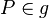 
gegeben.
Beweisen Sie:
Aufgabe 9.08
Formulieren Sie die Aussagen 1 und 2 aus der vorangegangenen Aufgabe 9.7 als einen einzigen Satz kurz und prägenant derart, dass auch Schüler der SI diesen Satz verstehen können.
Aufgabe 9.09
Beweisen Sie:
- Wenn im Inneren des Winkels liegt, dann ist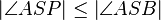
.
- Wenn
Aufgabe 9.010
Beweisen Sie:
- Jeder Winkel hat genau eine Winkelhalbierende.
