Ideen Aufgabensatz 3 Übung Heckl (SoSe2012)
Inhaltsverzeichnis |
Aufgabe 3.1
Unter einer Konventionaldefinition versteht man eine Definition, die in der Form "Wenn-Dann" formuliert wurde.
Geben Sie zwei prinzipiell verschiedene Konventionaldefinitionen des Begriffs Mittelsenkrechte einer Strecke an.
Wenn eine Strecke  einen Punkt M besitzt und gilt, dass
einen Punkt M besitzt und gilt, dass 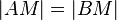 , und eine Gerade g
, und eine Gerade g  in den Punkt M im rechten Winkel schneidet, dann ist diese Gerade Mittelsenkrechte von
in den Punkt M im rechten Winkel schneidet, dann ist diese Gerade Mittelsenkrechte von  .
.
Wir setzen ebene Geometrie voraus. Sei M eine Menge von Punkten. Wenn M alle und nur die Punkte P enthält für die gilt, dass sie zu den Endpunkten der Strecke  jeweils ein und den gleichen Abstand, dann heißt M Mittelsenkrechte der Strecke
jeweils ein und den gleichen Abstand, dann heißt M Mittelsenkrechte der Strecke  .
.
Aufgabe 3.2
a)Ergänzen Sie so, dass sowohl die Hin- als auch die Rückrichtung wahr sind:
Wenn ein Viereck ein/e ... ist, halbieren sich seine Diagonalen.
Wenn sich die Diagonalen eines Vierecks halbieren, so ist es ein/e ...
b)Formulieren sie eine Äquvalenz.
c)Definieren Sie die Vierecksart durch das gefundene Kriterium.
Aufgaben zu Sätzen und Beweisen
Aufgabe 3.3
Wir gehen von folgender Implikation aus: Wenn zwei Geraden g und h nicht identisch sind, dann haben sie höchstens einen Punkt gemeinsam.
a) Wie lautet die Kontraposition dieser Implikation?
b) Wie lautet die Annahme, wenn Sie diese Implikation durch einen Widerspruch beweisen möchten?
Aufgabe 3.4
Satz: In einem Dreieck  mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
a) Welcher Beweis ist korrekt? Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)
Beweis 1)
Sei  ein Dreieck.
ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Da nach Voraussetzung |AC| ≠ |BC| gilt nach dem Basiswinkelsatz |α| ≠ |β|. Damit ist der Satz bewiesen.
Beweis 2)
Sei  ein Dreieck.
ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Nach Umkehrung des Basiswinkelsatzes gilt: Wenn |α|= |β| dann gilt |AC|= |BC|. Die Kontraposition der Umkehrung lautet also: Wenn |AC| ≠ |BC| dann gilt |α| ≠ |β|. Da die Kontraposition gleichwertig ist, kann man auch diese beweisen. Da nach Voraussetzung gilt: |AC|< |BC|, d.h. |AC| ≠ |BC|, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: |α| ≠ |β|. Damit ist der Satz bewiesen.
b) Beweisen Sie den Satz indirekt mit Widerspruch.
Und hier noch unsere Tafelanschriebe dieses Beweises. So haben wir ihn in der Veranstaltung geführt:

Im Anschluss an die Veranstaltung haben wir (ein paar Studierende und ich) wie angeboten noch eine zweite Beweismöglichkeit durchgeführt. Diese ist eigentlich unmittelbar einsichtiger:
--Flo60 17:26, 10. Mai 2012 (CEST)
Aufgabe 3.5
Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: 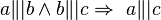 .
.
--Flo60 17:29, 10. Mai 2012 (CEST)
b) Welche Eigenschaft der Relation  auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?
Die Transitivität der Parallel-Relation
Zurück zur Übersicht
--Flo60 13:56, 9. Mai 2012 (CEST)



