Innenwinkelsatz für Dreiecke und starker Außenwinkelsatz (WS10/11)
Aus Geometrie-Wiki
Inhaltsverzeichnis |
"Der Abreißbeweis"
Diskutieren Sie Sinn und Unsinn des folgenden "Beweises":
http://www.ph-heidelberg.de/wp/gieding/Lehre/didaktik_5_8/flash/innenwinkelsumme.swf
sinnvoll, da es zu einer Geraden  durch einen Punkt
durch einen Punkt 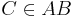 genau eine Gerade
genau eine Gerade  gibt für die gilt:
gibt für die gilt: 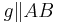 .
.
Durch Anwenden des Wechselwinkelsatzes auf die Winkel  und
und  erhält man die Winkel
erhält man die Winkel 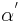 und
und 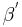 und dann mithilfe des Winkeladditionsaxioms und des Supplementaxioms die Gleichung
und dann mithilfe des Winkeladditionsaxioms und des Supplementaxioms die Gleichung 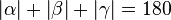 --Jbo-sax 11:03, 24. Jan. 2011 (UTC)
--Jbo-sax 11:03, 24. Jan. 2011 (UTC)
Ein echter Beweis
Satz XII.4: (Innenwinkelsatz für Dreiecke)
- Es sei
 ein Dreieck mit den Innenwinkeln
ein Dreieck mit den Innenwinkeln 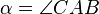 ,
, 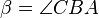 und
und 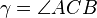 .
.
Es gilt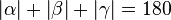 .
.
- Es sei
Beweis von Satz XII.4 (Innenwinkelsatz für Dreiecke)
Übungsaufgabe
Satz XII.5: (Starker Außenwinkelsatz)
- Jeder Außenwinkel eines Dreiecks ist so groß, wie die Summe der größen der beiden nicht anliegenden Innenwinkel dieses Dreiecks.
Beweis von Satz XII.5: (Starker Außenwinkelsatz)
Übungsaufgabe

