Lösung von Aufg. 12.2 SS11

Formulieren Sie den Basiswinkelsatz (Satz VII.5) auf zwei weitere Arten und Weisen.
Ich hoffe ich habe die Aufgabe richtig verstande.
Basiswinkelsatz V1:
Sei $\overline{ABC}$ ein gleichschenkliges Dreieck$\Rightarrow$ die Basiswinkel sind kongruent.

Basiswinkelsatz V2:
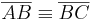Sei $\overline{ABC}$ ein Dreieck, wenn $\overline{AB} \equiv \overline{BC}$ dann gilt $\angle CAB\equiv \angle BCA$.
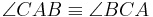--Peterpummel 21:01, 2. Jul. 2011 (CEST)

In jedem gleichschenkligen Dreieck ist die Mittelsenkrechte der Basis eine Spiegelachse. Triff dies den Kern des Basiswinkelsatzes? --Koooky 15:45, 6. Jul. 2011 (CEST)

Vielleicht ist hier auch einfach Konventional- und genetische Definition gemeint, so z.B.
V1: Wenn ein Dreieck gleichschenklig ist, sind seine Basiswinkel kongruent.
(wäre ja auch Lesweise von peterpummels Version 1)

V2: Konstruiere ein Dreieck mit zwei gleich langen Seiten. Die Basiswinkel dieses Dreiecks sind kongruent.

Allerdings macht eine so knappe genetische Definition hier m.E. keinen Sinn. Wenn ich tatsächlich gedanklich konstruiere, ist es nicht hilfreich, ohne nähere Erläuterung und Bezug auf eben die Konstruktion mit dem Begriff Basiswinkel zu arbeiten. Wie sehen die anderen das? --WikiNutzer 14:53, 7. Jul. 2011 (CEST)

Hier (Aufgabenstellung) ist ein Satz gefragt, keine Definition. Wo liegt der Unterschied?
Sind deine beiden "Definitionen" jetzt Sätze oder Definitionen? Warum macht eine Konstruktion wenig Sinn? --Tutorin Anne 16:48, 8. Jul. 2011 (CEST)