Lösung von Aufg. 7.2 (SoSe 11)
Oberstudienrat Kramer beginnt die Stunde zur analytischen Geometrie mit der Frage, ob denn jemand wüsste, wie eine Gerade im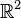 
definiert wäre. Vergleichen Sie mit Aufgabe 1.
Wird aber nicht in der analytischen Geometrie, eine Grade als eindimensionaler Untervektorraum definiert?--Peterpummel 12:07, 23. Mai 2011 (CEST)
Wird in de analytischen Geometrie mit Vektoren gearbeitet? Was ist eigentlich ein Untervektorraum?--Tutorin Anne 17:33, 24. Mai 2011 (CEST)
Ich hätte jetzt darauf getippt, dass Geraden im 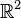in der analytischen Geometrie bestimmte Eigenschaften haben, vor allem die gleichbleibende Steigung, und dass bestimmte Funktionstypen eben Geraden als Graphen haben. Wenn man davon ausgeht, dass die analytische Geometrie mit dem Koordinatensystem eine "Frucht" der "normalen" Geometrie ist und dass letztere wiederum von uns auf Axiomen aufgebaut ist, dann wäre vielleicht eher z.B. die lineare Funktion über den Begriff der Geraden definiert und nicht die Gerade über die Funktion. So gesehen, wäre es dann vielleicht ein Geraden-Satz, keine Definition, zu sagen "Graphen von linearen Funktionen sind Geraden". Oder liege ich völlig daneben und analytische Geometrie ist etwas ganz anderes? --WikiNutzer 19:53, 24. Mai 2011 (CEST)
Der Vergleich der analytischen Geometrie mit einer "Frucht der Euklidischen Geometrie" ist gar nicht schlecht. Wenn ich Ihre Aussage mal dahingehend
interpretiere, dass Sie die analytische Geometrie als ein Modell der Euklidischen Geometrie ansehen, dann haben Sie Recht. Im Rahmen eines Modells
kann ich die Begriffe dann wieder genau definieren. Anderes Beispiel: In der Vorlesung hatte ich kurz gezeigt, dass ein Tetraeder aufgebaut aus
Trinkröhrchen ein Modell für Punkte (Ecken des Tetraeders) Geraden (Kanten des Tetraeders) und Ebenen (Seitenflächen des Tetraeders) sein kann. Ecken,
Kanten und Ebenen eines Tetraeders sind Begriffe, die Sie dann wieder genau definieren können.--Schnirch 14:47, 9. Jun. 2011 (CEST)
Im 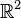läßt sich eine Gerade wie folgt definieren:
