Lösung von Aufg. 9.6 (SoSe 11)

Formulieren Sie die Kontraposition der Implikation aus Aufgabe 9.5.

Wenn der Durschnitt (= Schnittmenge) zweier Mengen nicht konvex ist, dann ist mindestens ein der Punktmenge auch nicht konvex.--Herbst2010 14:30, 8. Jun. 2011 (CEST)
Hört sich gut an! Muss man mindestens schreiben?
Allgemeine Frage: Habt ihr nicht konvexe Mengen in der Vorlesung als konkav definiert?--Tutorin Anne 11:17, 11. Jun. 2011 (CEST)

Anmerkung:
Seien M1 und M2 Punktmengen. Wenn 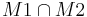$\ M1 \cap M2$ konkav $\Rightarrow \ M1 \vee M2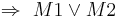$ konkav.
@Anne. Nicht konvex als konkav wurde in der Vorlesung meiner Meinung nach mündlich definiert. Es gibt nur verschiedene Lehrbücher in denen nicht konvex, nicht gleich konkav bedeutet. Siehe z.B Prof. A. Stevens "Analysis I", Script SS08, UNI HD. Dort gibt es Mengen die weder konvex noch konkav sind. Ist aber eine reine Definition Sache. Wir haben das sauber bei Herr Gieding definiert. --Peterpummel 17:45, 19. Jun. 2011 (CEST)