Lösung von Aufgabe 1.1 (SoSe 12)
Handelt es sich um Definitionen? Wenn ja, um welche Art von Definition (Real-, Konventional-, genetisch)? Begründen Sie!
- Jedes n-Eck mit n=4 heißt Viereck.
- Stufenwinkel an geschnittenen Parallelen sind kongruent.
- Eine Gerade heißt Dreiecksschneidende, falls es ein Dreieck gibt, dessen drei Seiten von der Geraden geschnitten werden, wobei die Eckpunkte des Dreiecks nicht zur Geraden gehören.
- Es gibt Vierecke mit einem Umkreis, die so genannten Sehnenvierecke.
- Wenn ein n-Eck vier Ecken hat, dann ist es ein Viereck.
- Es gibt Sehnenvierecke.
- Jeder Peripheriewinkel über einem Durchmesser ist ein Rechter.
- Ein rechter Winkel ist ein solcher, der zu einem seiner Nebenwinkel kongruent ist.
- Wenn ein Winkel zu einem seiner Nebenwinkel kongruent ist, so ist er ein Rechter.
- Ein Viereck, das so aussieht wie die Vierecke auf der bayrischen Fahne, heißt Raute.
- Es seien a und b zwei nichtidentische zueinander parallele Geraden. Lege auf a und b jeweils zwei verschiedene Punkte fest. Verbinde die vier Punkte zu einem konvexen Viereck. Du erhältst ein Trapez.
- Die Menge aller Punkte, die von den Endpunkten einer Strecke ein und denselben Abstand hat, heißt Mittelsenkrechte der Strecke.
- Eine Gerade, die senkrecht auf einer Strecke steht und diese halbiert, heißt Mittelsenkrechte der Strecke.
- Ein Rechteck hat vier rechte Innenwinkel.
- Jedes Quadrat ist ein Rechteck.
- Eine Raute ist ein Viereck mit vier gleich langen Seiten wobei je zwei Seiten parallel zueinander sind.
1. Realdefinition von Viereck
2. Stufenwinkelsatz
3. keine Def.
4. beweisbar, keine Def.
5. Konventionaldefinition
6. keine Def.
7. Satz des Thales
8. Realdefinition
9. Konventionaldefinition
10. intuitive Realdefinition
11. genetisch, operative Definition
12. Realdefinition
13. Realdefinition
14. keine Def.
15. keine Def.
16. informelle Definition--Alto1000 17:09, 24. Apr. 2012 (CEST)
Nr. 3 ist eine Definition. Es ist zwar falsch, da es keine Dreiecksschneidende gibt, die wir kennen, aber die Definition dafür ist richtig. (wurde heute in der Übung gesagt)xxx???xxx24. Apr. 2012 (CEST)
- - - - - - - - -
Kommentar:
Achtung bitte, wir hatten in der Übung nicht gesagt das die Definition falsch ist, sondern dass sie sinnlos ist, da wie du sagst uns keine Dreiecksschneidende bekannt ist. Die Begründung von Kopernikus ist korrekt - nicht richtig oder falsch sondern sinnvoll oder sinnlos --Tutor Dominik 21:38, 24. Apr. 2012 (CEST)
@ Tutor Und warum ist dann ist Aufgabenstellung bei der Definition 1.3 mit richtig bezeichnet? Wurzel
Wurzel: Ich empfehle dir nochmals das Kapitel Definieren in der Mathematik durchzulesen.
Entscheidend ist die Frage, ob die Definition das definiert was sie definieren soll. Ich möchte an dieser Stelle nicht explizit auf die Aufgabe 1.3 eingehen. Sofern allerdings die Definition eines Kreises gefordert ist und die Definition dann eine Kugel beschreibt, ist dies natürlich falsch bzw. ich würde eher sagen die Aufgabenstellung nicht erfüllt.
Hmmmm ich schreib mal noch ne Begründung bei ein paar Sachen dazu und Nr. 3 sehe ich so wie der Namenlose vor mir.
Nr 2 ist keine Def ist ein Satz. Also wahr oder falsch und keine Def.
Nr 3 ist eine Def. allerdings eine sinnlose
Def sind nie falsch, nur sinnvoll oder sinnlos
Nr.7 ist keine Def. ist ein Satz also wahr oder falsch
Nr 14 hätte ich eine intuitive Realdef. gesagt.--Kopernikus 21:31, 24. Apr. 2012 (CEST)
Kommentar M.G.
- Zu Nr. 14: Ein Rechteck hat vier rechte Innenwinkel. Könnte das wirklich eine Definition sein? Überlegen Sie: Weiß jemand nachdem ihm 14 mitgeteilt wurde, was ein Rechteck ist? Man weiß doch nur: Falls man es mal mit einem Rechteck zu tun haben sollte, dann hat dieses Ding vier rechte Innenwinkel. Das Verb
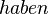 ist kaum für eine Definition gegeignet. Entweder ich habe etwas oder ich habe dieses etwas nicht. Per Definition kommen nur Gurus und Selbstdarsteller (etwa Wolf Christoph Fuss) zu dem gewissen Etwas. Der Rest muss (z.B. bei der Partnerwahl) beweisen, dass er über das gewisse Etwas verfügt. eine Definition ist immer in gewisser Weise eine Namengebung. Es solte also möglich sein, den Sachverhalt aus 14 mittels des Verbs heißen zu formulieren. Ein Rechteck mit vier rechten Innenwinkeln heißt??? Wir sehen, es fehlt ein Oberbegriff: Ein Viereck mit vier rechten Innenwinkeln hat ein Rechteck: Ich weiß wo dein Haus wohnt. Was geht: Ein Viereck mit vier rechten Innenwinkeln heißt (ist ein) Rechteck.
ist kaum für eine Definition gegeignet. Entweder ich habe etwas oder ich habe dieses etwas nicht. Per Definition kommen nur Gurus und Selbstdarsteller (etwa Wolf Christoph Fuss) zu dem gewissen Etwas. Der Rest muss (z.B. bei der Partnerwahl) beweisen, dass er über das gewisse Etwas verfügt. eine Definition ist immer in gewisser Weise eine Namengebung. Es solte also möglich sein, den Sachverhalt aus 14 mittels des Verbs heißen zu formulieren. Ein Rechteck mit vier rechten Innenwinkeln heißt??? Wir sehen, es fehlt ein Oberbegriff: Ein Viereck mit vier rechten Innenwinkeln hat ein Rechteck: Ich weiß wo dein Haus wohnt. Was geht: Ein Viereck mit vier rechten Innenwinkeln heißt (ist ein) Rechteck.
- Zu Nr. 14: Ein Rechteck hat vier rechte Innenwinkel. Könnte das wirklich eine Definition sein? Überlegen Sie: Weiß jemand nachdem ihm 14 mitgeteilt wurde, was ein Rechteck ist? Man weiß doch nur: Falls man es mal mit einem Rechteck zu tun haben sollte, dann hat dieses Ding vier rechte Innenwinkel. Das Verb
"Haben" weist immer auf eine Existenzaussage hin. Definitionen sind keine mathematischen Aussagen, also können Definitionen nicht als Existenzaussage formuliert werden.
Nicht zu verwechseln damit, dass die Existenz einer bestimmten Eigenschaft im Rahmen einer Definition als wahr vorausgesetzt wird: Wenn ein Viereck vier rechte Innenwinkel hat, dann heißt es Rechteck.--*m.g.* 11:35, 26. Apr. 2012 (CEST)
Frage: Kann ich bei der 5. sagen, dass es eine Konventionaldefinition ist, die aber nicht sinnvoll ist. Immerhin können auch Fünfecke vier Ecken haben, sind aber dann ein Fünfeck und kein Viereck!? --Honeydukes 11:52, 30. Apr. 2012 (CEST)

