Lösung von Aufgabe 1.2 (SoSe 20)

Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.

$M_1 = \{x\vert x\in \mathbb{N}\wedge x+2 = 0\}$

$M_2 = \{x\vert x\in \mathbb{R}\wedge x^{2}+2 = 0\}$

$M_3 = \{x\vert x\in \mathbb{Z}\wedge x+2 = 0\}$

$M_4 = \{x\vert x\in \mathbb{Q}\wedge x^{2}-2 = 0\}$

$M_5 = \{x\vert x\in \mathbb{R}\wedge x^{2}-2 = 0\}$

$M_6 = \{x\vert x\in \mathbb{R}\wedge (x+2)^{2} = 0\}$

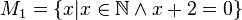
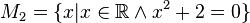
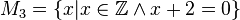
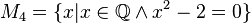
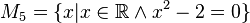
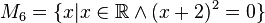
Lösungen:
M_1, M_2 und M_4 ergeben keine Lösung; M_3,M_6: x=-2 -> sie sind identisch; M_5: x=+- Wurzel (2) --Kohfahlm (Diskussion) 17:18, 22. Apr. 2020 (CEST)

Richtig. Man sagt auch $M_1$, $M_2$ & $M_4$= Ø (leere Menge)
Damit die Zahlen nach unten versetzt werden, muss man das zwischen $...$ stehen. 
Mathematische Formeln werden im Wiki mit $....$ eingerahmt.
Weitere Infos unter: http://geometrie.zum.de/wiki/Formeln_verwenden
Da kann man mit etwas Zeit ein wenig herumprobieren.--Tutorin Laura (Diskussion) 20:20, 22. Apr. 2020 (CEST)