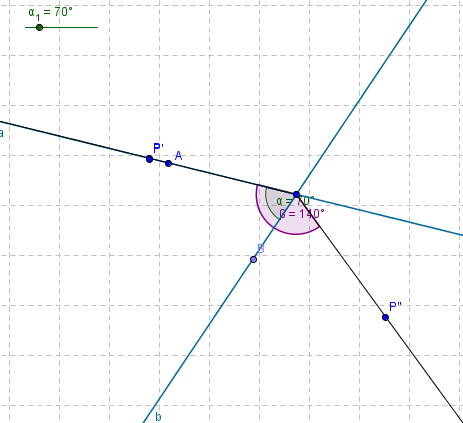
Lösung von Aufgabe 10.3P (WS 12 13)

Welche wichtige Erkenntnis ergibt sich aus Satz IX.2 für die absolute und relative Lage der beiden Spiegelgeraden? Nutzen Sie diese Erkenntnis für die Lösung der folgenden beiden Aufgaben.

Satz IX.2
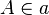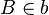Gegeben seien zwei Spiegelgeraden a und b mit einem gemeinsamen Schnittpunkt S, sowie zwei Punkten $A\in a$ und $B\in b$, die von S jeweils verschieden sind. Wir betrachten die Verkettung $S_{a}\circ S_{b}$. Für einen beliebigen Punkt P und seinen Bildpunkt $P''=S_{a}\circ S_{b}(P)$ gilt: $\left| \angle PSP'' \right| =2\cdot\left| \angle ASB \right|$.

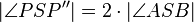Erkenntnis von Kaeseknilch

Wenn der Punkt P beliebig zu wählen ist, darf er doch auch auf a oder b liegen oder? Also auch im Punkt A, bzw. Punkt B.

Das würde dazu führen, dass Kein Dreieck entstünde, somit auch keine Vergleichbaren Winkel zu Stande kommen und der Satz IX.2 nicht für jedes beliebige P gelten kann.

Muss hier noch ein Zusatz vorgenommen werden im Satz selbst oder bin ich mit meinen Gedanken auf einem Holzweg und wenn ja warum? --Kaeseknilch 14:29, 23. Jan. 2013 (CET)

• Ich weiß nicht von welchem Winkel du sprichst bzw. von welchem Dreieck. Ich sehe kein Problem in dem Fall, dass z.B. P auf A oder auf der Gerade a liegt.--Tutorin Anne 13:08, 24. Jan. 2013 (CET)
  

Danke Anne, hast meine Gedanken wieder geordnet, hatte einfach eine falsche Vorstellung im Kopf bzw. das Blatt falsch gesehen! Danke auch für die GeoGebra-Applikation! --Kaeseknilch 15:52, 24. Jan. 2013 (CET)

P und A sind verschiebbar - du kannst verschiedene Fälle durchspielen.

weitere Erkenntnisse

• Die Aufgabe ist noch nicht gelöst, tragt hier weitere Vorschläge ein.--Tutorin Anne 13:11, 24. Jan. 2013 (CET)