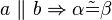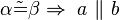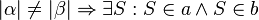Lösung von Aufgabe 3.3 (WS 14/15)

a) Wie lautet der Stufenwinkelsatz? (schauen Sie bei Bedarf in Schulbüchern nach).
b) Es seien a und b zwei nichtidentische Geraden, die durch eine dritte Gerade c jeweils in genau einem Punkt geschnitten werden. Bei diesem Schnitt entstehen die Stufenwinkel $\alpha$ und $\beta$. Welche der folgenden Aussagen repräsentiert den Stufenwinkelsatz bzw. ist eine zu diesem Satz äuivalente Aussage (Begründen Sie jeweils)?

1. $\ a \ \| \ b \Rightarrow \alpha \tilde {=} \beta$
2. $\alpha \tilde {=} \beta \Rightarrow \ a \ \| \ b$
3. $\left|\alpha \right|\not= \left| \beta \right| \Rightarrow \exists S: S \in a \wedge S \in b$
4. $\ a \ \| \ b \Leftrightarrow \alpha \tilde {=} \beta$

 A) Wenn zwei parallele Geraden a und b von einer dritten Geraden c geschnitten werden, so sind die auftretenden Stufenwinkel gleich groß.
  B) 1) korrekt, repräsentiert den Stufenwinkelsatz
       2) Umkehrung des Stufenwinkelsatzes, kein Repräsentant, des SWS da dessen Umkehrung noch nicht bewiesen ist
       3) Kontraposition des Stufenwinkelsatzes --> gleichwertig zum Satz, äquivalente Aussage 
       4.) kein Repräsentant des Stufenwinkelsatzes, gilt erst, wenn 2. bewiesen wurde--Leuchtbärli (Diskussion) 19:49, 24. Nov. 2014 (CET)