Aufgabe 3.4
Wir stellen den enaktiven "Beweis" vom Kopf auf die Füße:
Satz (*): Es sei  ein Dreieck. ein Dreieck.
Wenn die Winkelpaare 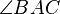 und und 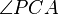 bzw. bzw.  und und 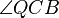 jeweils zueinander kongruente Wechselwinkel sind, jeweils zueinander kongruente Wechselwinkel sind,
dann gehören die Punkte 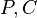 und und  ein und derselben Geraden an. ein und derselben Geraden an.
Führen Sie einen Widerspruchsbeweis für Satz (*).
Hilfe: Es gelten die folgenden Aussagen:
- Umkehrung des Wechselwinkelsatzes: Wenn beim Schnitt zweier Geraden
 und und  durch eine dritte Gerade durch eine dritte Gerade  kongruente Wechselwinkel entstehen, dann sind kongruente Wechselwinkel entstehen, dann sind  und und  zueinander parallel. zueinander parallel.
- Euklidisches Parallelenaxiom: (alles in der Ebene) Durch einen Punkt
 außerhalb der Geraden außerhalb der Geraden  gibt es höchsten eine Parallele zu gibt es höchsten eine Parallele zu  . .
Lösung von User Caro44
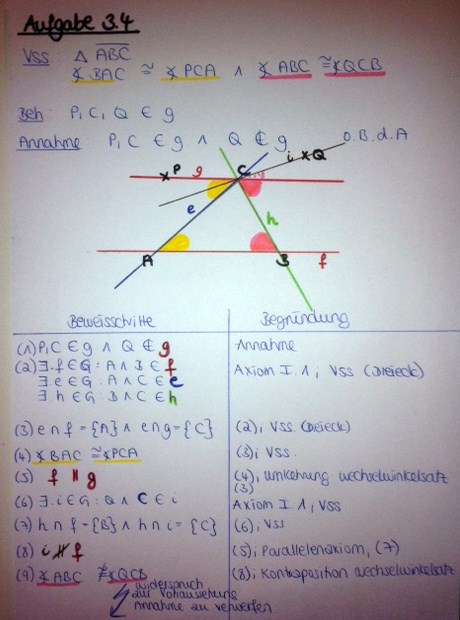 --Caro44 14:22, 14. Nov. 2012 (CET)
--Caro44 14:22, 14. Nov. 2012 (CET)
Lösung von User ...

--B..... 10:30, 15. Nov. 2012 (CET)
|  ein Dreieck.
ein Dreieck. 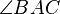 und
und 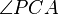 bzw.
bzw.  und
und 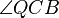 jeweils zueinander kongruente Wechselwinkel sind,
jeweils zueinander kongruente Wechselwinkel sind, 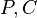 und
und  ein und derselben Geraden an.
ein und derselben Geraden an.
 und
und  durch eine dritte Gerade
durch eine dritte Gerade  kongruente Wechselwinkel entstehen, dann sind
kongruente Wechselwinkel entstehen, dann sind  außerhalb der Geraden
außerhalb der Geraden  gibt es höchsten eine Parallele zu
gibt es höchsten eine Parallele zu 


