Aufgabe 3.9 SoSe 2018
Die folgende Aussage möge wahr sein:
(I) Durch zwei verschiedene Punkte geht genau eine Gerade.
Wir betrachten den folgenden Satz:
- Wenn zwei Geraden
 und und  nicht identisch sind, dann haben Sie nicht mehr als einen Punkt gemeinsam. nicht identisch sind, dann haben Sie nicht mehr als einen Punkt gemeinsam.
(a) Beweisen Sie den Satz, indem Sie seine Kontraposition beweisen.
(b) Beweisen Sie den Satz mittels eines Widerspruchsbeweises.
Lösung 1

Kommentar --*m.g.* (Diskussion) 15:31, 10. Jun. 2018 (CEST):
Formulierungsschwächen
Die Kontraposition
Die Kontraposition wurde prinzipiell richtig gebildet. Das rein formale Umkehren und Negieren passt jedoch mitunter nicht für eine korrekte Formulierung:
"Wenn mehr als ein Punkt gemeinsam, dann sind zwei Geraden identisch."
- Wer hat mehr als einen Punkt gemeinsam?
- Um welche Geraden geht es in der Behauptung?
Korrekte Formulierung:
Wenn zwei Geraden mehr als einen Punkt gemeinsam haben, dann sind sie identisch.
Ihre Formulierung:
Irgendwelche nicht spezifizierte Objekte (etwa ein Kreis und eine Strecke) haben mehr als einen Punkt gemeinsam. Daraus folgt: Irgendwelche zwei Geraden sind identisch.
Der Beweis der Kontraposition
Sie schreiben: Es existieren zwei Punkte 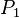 und und 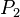 und zwei Geraden und zwei Geraden 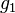 und und 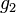 . .
Das sagt der Satz "Wenn zwei Geraden zwei Punkte gemeinsam haben, dann ... " jedoch nicht aus:
"Es gibt zwei Geraden, die zwei Punkte gemeinsam haben." ist mit dem Satz nicht gemeint. Der Satz meint: "Sollten zwei Geraden zwei punkte gemeinsam haben ... " bzw. "Falls zwei Geraden zwei Punkte gemeinsam haben ...". Sie dürfen damit den beweis nicht mit den folgenden Worten beginnen: "Es gibt zwei verschiedene Punkte, die auf zwei Geraden liegen." In diesem Fall hätten wir einen Existenzbeweis zu führen. Wir haben aber zu zeigen, dass unter der Bedingung, dass zwei Geraden zwei (verschiedene) Punkte gemeinsam haben, eben diese Geraden identisch sind.
Der Beginn des Beweises lautet also:
Wir gehen davon aus, dass zwei Geraden zwei verschiedene Punkte gemeinsam haben.
Oder anders formuliert:
Es seien 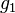 und und 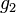 zwei Geraden, die zwei verschiedene Punkte zwei Geraden, die zwei verschiedene Punkte 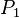 und und 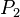 gemeinsam haben. gemeinsam haben.
oder wenn wir mit den gemeinsamen Punkten beginnen wollen:
Es seien 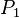 und und 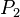 zwei verschiedene Punkte, die die beiden Geraden zwei verschiedene Punkte, die die beiden Geraden 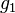 und und 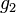 gemeinsam haben. gemeinsam haben.
ansonsten ist die Schlußfolgerung korrekt.
Der Widerspruchsbeweis
Hier geht alles drunter und drüber. Ausgangspunkt ist die ursprüngliche Implikation.
Wenn zwei Geraden  und und  verschieden (nicht identisch) sind, dann haben sie nicht mehr als einen Punkt gemeinsam. verschieden (nicht identisch) sind, dann haben sie nicht mehr als einen Punkt gemeinsam.
Voraussetzung:  und und  sind nicht identisch. sind nicht identisch.
Behauptung: Es gibt nicht mehr als einen Punkt, den  und und  gemeinsam haben. gemeinsam haben.
Der Widerspruchsbeweis geht davon aus, dass die Vorauusetzung wahr, die Behauptung jedoch falsch ist.
Wir nehmen also an, dass die beiden Geraden  und und  zwar verschieden sind, aber mehr als einen Punkt gemeinsam haben .... zwar verschieden sind, aber mehr als einen Punkt gemeinsam haben ....
|  und
und  nicht identisch sind, dann haben Sie nicht mehr als einen Punkt gemeinsam.
nicht identisch sind, dann haben Sie nicht mehr als einen Punkt gemeinsam.
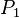 und
und 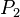 und zwei Geraden
und zwei Geraden 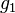 und
und 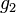 .
.
