Lösung von Zusatzaufgabe 2.1P (WS 12 13)

Definieren Sie den Begriff gleichschenkliges Trapez. Beachten Sie dabei, dass ein Parallelogramm dann und nur dann ein gleichschenkliges Trapez ist, wenn es einen rechten Innenwinkel besitzt.

Ein gleichschenkliges Trapez ist ein Trapez, bei dem die nicht parallelen Seiten kongruent zueinander sind. --Der Bohrer 10:46, 22. Nov. 2012 (CET)

• Diese Definition stimmt nicht. Warum? Und wo liegt der Fehler? Wie lautet eine korrekte Definition?--Tutorin Anne 15:31, 22. Nov. 2012 (CET)

Die Lösung stimmt nicht, weil dies auch für die Parallelogramme gilt.

• Nein, das ist nicht die richtige Begründung. Diese Definition schließt allerdings z.B. Rauten mit ein - vielleicht hast du das gemeint?--Tutorin Anne 22:11, 5. Jan. 2013 (CET)

Rauten sind auch Parallelogramme...--Unicycle 15:59, 19. Jan. 2013 (CET)

Wenn er schreibt: Die nicht parallelen Seiten sind kongruent zueinander. Schließt das nicht das Parallelogramm aus? Denn da sind die kongruenten Seiten parallel zueinander. --Unicycle 15:59, 19. Jan. 2013 (CET)

• Richtig, er schließt Parallelogramm aus. Rauten aber nicht, denn sie haben kongruente nicht parallele Seiten und eine Raute ist keine gleichschenkliges Trapez. Damit ist die Defninition nicht korrekt. --Tutorin Anne 12:47, 20. Jan. 2013 (CET)
• Tipps zum Schreiben einer Definition:
  

1) Mache dir bewusst welche Eigenschaften das Objekt hat.
2) Welche Oberbegriffe gibt es?
3) Welche Unterbegriffe d.h. in unserem Fall: Welche Vierecksarten gehören zum Begriff dazu und dürfen nicht ausgeschlossen werden?
4) Zu welchen ähnlichen Begriffen muss ich mich eindeutig abgrenzen? (Hier: Welche Vierecksarten dürfen nicht enthalten sein).
5) Definition schreiben und v.a. an Punkt 3 und 4 überprüfen, ob sie stimmen kann.
Auch ich muss jede Definition, die ich mir so ausdenke 2- 3 mal umschreiben, weil ich was vergessen habe oder falsch beschrieben habe - wichtig ist, dass es einem halt auffällt!--Tutorin Anne 12:47, 20. Jan. 2013 (CET)

Ein gleichschenkliges Trapez ist ein Trapez mit zwei paar gleich großer benachbarter Winkel--RM2208 15:11, 1. Feb. 2013 (CET)
Die Definition ist richtig. Wichtig ist, dass man dieses "zwei Paar" Winkel nennt, denn nur ein Paar genügt nicht. Hier seht ihr nämlich ein Gegenbeispiel, mit nur einem Paar gleich großer Winkel.--Tutorin Anne 17:48, 1. Feb. 2013 (CET)

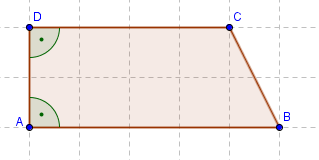
Was soll das eigentlich heißen? "Beachten Sie dabei, dass ein Parallelogramm dann und nur dann ein gleichschenkliges Trapez ist, wenn es einen rechten Innenwinkel besitzt." --> Wie kann ein Parallelogramm einen rechten Innenwinkel besitzen? --RM2208 15:12, 1. Feb. 2013 (CET)

Welche Vierecke mit einem rechten Winkel sind sowohl gl. Trapez und auch Parallelogramm?--Tutorin Anne 17:40, 1. Feb. 2013 (CET)

Rechteck und Quadrat? --RM2208 18:08, 1. Feb. 2013 (CET)

Ich verstehe aber auch nicht den Zusammenhang zwischen Parallelogramm und gleichsch. Trapez.... Das sind doch 2 versch. Vierecke. Und warum wird sich bei dem Parallelogramm auf das mit dem "einen rechten Innenwinkel" bezogen? --RM2208 18:12, 1. Feb. 2013 (CET)
Also, dieser Hinweis ist vielleicht eher verwirrend als hilfreich. Es geht darum, dass ja das Rechteck (eingeschlossen Quadrat) auch zu dem gl. Trapez gehört... das muss beachtet werden. Das heißt z.B., das man nicht von "nicht parallelen Seiten" sprechen kann, ohne das Rechteck auszuschließen. --Tutorin Anne 15:09, 2. Feb. 2013 (CET)