Übung Aufgaben 1 (WS 20 21)
Inhaltsverzeichnis |
Mengenlehre
Bitte beschäftigen Sie sich mit der Mengenlehre. Arbeiten Sie das Skript zur Mengenlehre durch. Außerdem stehen Ihnen bei YouTube die Videos der Vorlesung "Mathematische Grundlagen 1" zur Verfügung:
Wir setzen diese Kenntnisse bei Ihnen voraus und werden nicht explizit auf die Inhalte in der Vorlesung eingehen.
Aufgabe 1.1
Es sei A die Menge der geraden natürlichen Zahlen, B die Menge der natürlichen Zahlen, deren Quadrate gerade ist. Vergleichen Sie die Mengen.
Lösung von Aufgabe 1.1 (WS_20_21)
Aufgabe 1.2
Geben Sie eine andere Schreibweise der folgenden Mengen an und prüfen Sie, welche Mengen identisch sind.
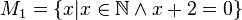
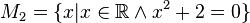
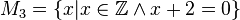
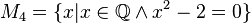
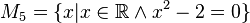
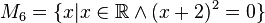
Lösung von Aufgabe 1.2 (WS_20_21)
Aufgabe 1.3
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen. Stellen Sie die Teilmengenbeziehungen in einem Venn.Diagramm dar.
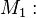 Menge aller gleichschenkligen Dreiecke
Menge aller gleichschenkligen Dreiecke
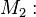 Menge aller gleichseitigen Dreiecke
Menge aller gleichseitigen Dreiecke
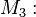 Menge aller gleichwinkligen Dreiecke
Menge aller gleichwinkligen Dreiecke
Lösung von Aufgabe 1.3 (WS_20_21)
Aufgabe 1.4
Prüfen Sie, welche der folgenden Mengen identisch sind und welche Teilmengenbeziehungen bestehen.
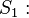 Menge aller Vierecke mit vier kongruenten Winkeln
Menge aller Vierecke mit vier kongruenten Winkeln
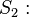 Menge aller Vierecke mit gleich langen, einander halbierenden Diagonalen
Menge aller Vierecke mit gleich langen, einander halbierenden Diagonalen
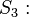 Menge aller Vierecke mit zwei Paaren paralleler Gegenseiten und einem rechten Winkel
Menge aller Vierecke mit zwei Paaren paralleler Gegenseiten und einem rechten Winkel
Lösung von Aufgabe 1.4 (WS_20_21)
Aussagenlogik
Bitte rufen Sie sich die Aussagenlogik ins Gedächtnis. Eine gute Wiederholung (bzw. eine gute Einführung, falls Sie die mathematischen Grundlagen 1 noch nicht besucht haben) finden Sie bei YouTube:
Aufgabe 1.5
Beweisen Sie jeweils mit einer Wahrheitstabelle:
-
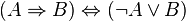
-
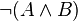
 (
(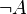
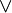
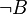 )
)

