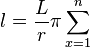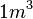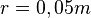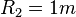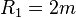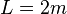Didaktik 08 - 10: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Realmodell) |
*m.g.* (Diskussion | Beiträge) (→Formel) |
||
| Zeile 82: | Zeile 82: | ||
<ggb_applet width="727" height="439" version="4.0" ggbBase64="UEsDBBQACAAIAK8BiT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAK8BiT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Z3pkhvJccc/y0/RMR8UdgQ57AsNYEXKQe5ytQqvbIW4Vjj8hYFBXxAwQF/DQ7bfxm/iF3M1Go1BH5nZCUzXcmZSoeXg6LP+v8oqVP676vU/f7ndGJ+CLF/ttm+urGvzygi2y52/2kZvru6K8OXs6p9//w+vo2AXBTfZwgh32e2ieHPllluu/DdXM2c6syaO/3LpqH/cm8XNy9nUtl9as9ncWcxuPG8+uzKML/nqu+3uXxe3QZ4slsGHZRzcLn7eLRfF/sRxUSTfvXr1+fPn6/pU17ssehVFN9dfcv/KUJe5zd9cHV58pw7X2Omzs9/cNk3r1X/86efq8C9X27xYbJfBlVHewt3q9//wm9efV1t/99n4vPKL+M3V1HWujDhYRbG6p8nUuzJelRslqkCSYFmsPgW52vXk7f6ei9vkar/ZYlt+/5vqlbE53s6V4a8+rfwgK4t0MlMF5Fm2M7Ntx7VUaeyyVbAtDttah3O+qo/2+tMq+Fwdtny1P6Pa6NMqX91sgjdX4WKTq1tabcNMFefxfV583QQ3i+z4wf3lqHvMV39Xm1rWTMlWFYF6Z5ovyv889Z9rmtV1nJzUvTKK3W6zP6Zp/Pd/G7Zpm8aL8o9V/bHVH8+rvjKrz0yn+mNXf9zqz6Taxq12d6tN3Wobt9qmVOJ4j0V2h95i9f39HVr1HU7t6fAbtB+oVM2eQrUn/ee0POSk1W0h5zzepzU5Oac61f7/+/86Z3Sw22yfESxYxgk9V8stvn5VV5TXB0yNPC63PcBTBLd5Ca4zNybzkj/LmChIvanCbWJYc/VnahsKS8OaGO5EvbVmhlf+nRrOVH3hGo4xM8rtLMfYUzqZqX/c6f5gnjFRBys/narKYVjqRK4xcQxrD7drKKSNfQVRlcV21BaTiTFRO5Wnt+zyEI5nuJ5658wMV11jWTemltrQUTuq9+r0tuFYhlPubE0N2zO88niWW9Y5b1ZeujqkbXim4VnlAVX1UlWrqlZq+5nhlHdTB7XVNrkrGkW0vPXrl8UuOWqhtlbR6D7mVdGpERJ/83qzuAk2qpX4UCppGJ8Wm7JG7E8U7raFUYtoV59F2SKJV8v8Q1AUaq/c+Nvi0+LnRRF8+VFtndfn3m+73G3zP2e74vvd5u52mxvGcrcxj9e821gnr+3jVas3zskX7ukXk5MvvJPX097z7tQ3xl0eqPPvsrzefOH7fyy3uA8NqiT/bbv5+i4LFutkt2rexutX+wbndXC33Kz81WL7VwVreZayXIy6/akCct0AzdxJfSW7zP/wNVcIG1/+M8h2ZVzxrudT1dqanj2ZW7aqJl+rb2zPvjbntu1OzanlOXN1ZcvFZh/tJ9fWZOY686k7tc3ZXNXLr8B302l15uDTUaHFl+B481FWVuzDjZdv/pi/223uP9rf/veLpLjL9j0HFRuz8p7ebqNNsEdkH21Vs7xc3+y+fKjYcKpj/fI1Ue/M6gJuon2xGyo02JOJ2uDw96b6u9+mvLLjVuZ+G3O/hVnDtvKP31tze7/F/u9N9Xe/laK3urTDnVr1bVpmfZpVvg9o5lWj2uzRLxv5u+2q+Ll+U6yW68OdWtX2/3p3exMcAWoe0nqgQ75+1QLsdZ4oHv08DoKiF7l9C1kT51pWdWFqp/D7YLP50Nj0hE37UGonh6/qZ307h30mM2w7+7idZVrYhs79hlMT29A92XCObTg5bujUlxhsyoC22xpG/GGZ7TabvdSfTl4v9/vvX2alWodL2Sy+7u7KGKck+VH1iO82i3f3rWf56R/2JN2//6k6aGurv/Z++k6dKg+yP6v+4KYRbaq7+UndXNDY4S/q+PsPjWOw2mx2nz+oeL1abN77q2J339Luv/pFNZi/rJJj/Q7SO/XtX9SfVRb4jah4WpoKkB/3PwCMww+BPy1Us2G+MF/cvLAm3zkvvOqF+8KuXqg+UPXCqr+y6xfmi5fWi8UL87uyv1R/Z9dbH15M6o2c+hP3fn+rfjGpTz+vt5nVu1vl7tWuL5YvXtoTT20/rU83r083rw/l1J/M6m1m9cFn9cGPG1tWvZFbf3QsAKvezayP6NYbH27Jql/YxwJw61uxTsrkeIBjKbv1i2Ph3B/g/pjHI9VfHaWY1IeeHK/WrG/gWMzHsx3vZFJvM68/mR73txpF7N6X47Gsp/VOTv2JdX+Jx4I87ufUJzuWf+cc1RGrKNiJeq/XQabqz6FdVy3a3e4ur7opJ3D7qobcqrfVF4cQtygbrX9Xgbj61A+iLKjj92b/27RqNvbfmqctdufj/aF+zHa3f9x++kW1iK0LeP2qvsrX+TJbJWXDa9yovvD6vhKqn5L5QnWlT2vlvquiam4VvYpVUTYRqmrfFXFZ09U+qmel/pb9jy+qZPLy533dyHyvgrX69M3Vb9O7XfG7vyz8lSqZ1da4rT7Yn0CFxlv1G9Uo9m2z6qYVVyf77+OCCjzG7uZvKoTe9+KrLU4KWG0AtNQqECXxQr26vg+qKoKdlt7+cH/a+adlqhq86tJ67+2H5r39+22oFDAC1dLnxr9kwSoPOHf6wzd8p++bd/ov5aeb//vfbaS6M3ehUTYGPy/Um+F3+/4bvtu3duNuyzsbdlNqx2/lphoXub27DbLV8ngV76rrVLveHQ5g1ad6uGu3Bl67VQcvFRv3EUb9EEmqPmgSBFV3rzh02o1EHW7f5z+5mMXdl9Vmtci+Vsc76awOLI7v+4pj8nzL44dOeXjXzvMtjvddPGzvideXbkx0zo2JziOJiU5bZfuJa4zHxE5xWNfWc46JnfLwrufPtzjed/FwZk+8vnRjontuTHQfSUx02yo7T1xjPCZ2isO6tp9zTOyUx/T6GRfH+y4eE/OJ15duTJycGxMnjyQmTtoqu09cYzwmdorDunaecRD4oVMes/rqn2NxvO/i4T3131XdmOidGxO9RxITvbbKkyeuMR4TO8VhXbvPOSZ2ymN2PX2+xfG+i8f0qfchujFxem5MnD6SmDjtDhg9bY3xmNgpDut68pxjYqc85s86x9LFY/bU60s3Js7OjYmzRxITZ90Bo6etMR4TO8VhXXvPOSZ2ymP+rHMsXTzmzy/HMj83Js4fSUycd38cPW2N8ZjYKQ7revqcY2K3PMxnnWTplIdtPb8ki2WeGxXVno8jLB4utNEZeNoy43GxWx7W9ewZB4IfegrEetaplm6B2Pbzy7VY1tmh8duxpBOh0erpEzxtnYnY2C2Q6/mzjo3dArGedcqlWyC28+xyLj9YzQdb/hDki9uieo5n6DNKIz3hgjyIfb/18ZHsh46o762uxX9mPvWY2uHjxxYfAx/l+nEsKB7mGb2mSbd6Ls9Ist3+ibXvhnL/SBy7P1gdw439xDle7m5vF1vf2O5nfPl+lS03wb4MqilIFuabq39URTB5YZRPdf2TugtrL8AhluzuinqzZXXowwE7Zb3cbU9KetkFojG7wpg8nE4nUcSr5XqroN/Pd3AszPLFTyvfD7ZHFYJVFGw/qSvdZblhfDHfVDNwfTWr8xt/rz/5ogro5f6jr9bho78fXuwPpLTMVl+Mt/X2b+ut3trlC8u0VeR+6xwO+9atjlZ+NlEv75+tC9JtdQ95Ne1EOeXLKlwtcYX/ur+DjsIvDPOgrVLb2r9r63uH61sVzVHAu1+zxh+e8c6NL1V1M77WIp0e6gwITh4dP5T6cpEVQb5abA9BolDv/1zOsGJUJzcbJz9AAMvzS7bY5ptF0a6Dy0qcu26t++0i2eW/Y9W9wy5SA4EaaPfVQGtiNv5nP1CFBBU/qITrfrb6wgDOgNfHgP1QUZgQnSH9hQAIBigGtgoFJ3Xe6iLhaEUCB8PnYOCL6IDojtkQ3e6K7rrzxv+8kRnwQcX51d+XKo+q7zbVd7rqT1rqjy0+UenPbQd8aQEG4DBptgBuFwfvV8GBAcWFaAggKCCeR8WL6a8ICI5JwIEiEAQABGY21WGY6UUgAAXnx4JA6j8ivn1tmlQDMW+KPxtbfKLOn9soBNIcDMDBbuLgtXFQm/4qODCguBANAQQFxLXx/sJ+oiiNSOBghBwMQhEdEL3VSewMLVrjDy2GoMT8+h5KHUflnpN1fPRhw5Co1+eG+lCCPAmAM6AX4DbTSWNnk8JBwf6yXkDf7gJIPyAT4ldD+Xh3AxBHJyA4JhEHikgQABBojRpMuwh4TQTckRGIQMH5sSCS+o+I7+7zy3iHcPptif/ROkP+jz3PBAgA3ygARNA/t1cQSX9gAA7NNFPHZ1A+rNagQaMdUL2+trp2wE84BC074Kdvxw5oHhx51uO3A37qqHJwi3y0OVX0fiepnoAlpNcSeFILW+5Aa4wI3XAEgtJfAIBgQGHg8pyhGqlgsHExIcIJxcmMcI9qBwPHI+egkIvskHXMZbhFdSDgQ4L758QAX+o9zyzGco5q4QEPA/757UN7VyGknxCPyAwh7lKNgDAwuRgWQYZAZuqe7UDVjgwOTsGBpBAgILvh7GzHqQ4gAkj+4JxYEUh8oAyIZHwA3adacMBjQnB+M9LeVQDpB6T1EFvHjIA4VDUCwsDkYlgEGZ5JccZwsWpHhhj54iUul5KyhE2MLpWytPQOb4SQ6OE5ESKUqEAA0Op49jhWNA9xhnjdD89vLtq7ChJ9SDjXFhkTNA959hgdCTAuxkMgISChexOgG1Y7MsTQF6834UtvAoRiSvwqQRywOqCIIARqa5vDAeF+J8GhDwd3P4rBcMBqQQCPBdH5zUd7V4GiH4q+PDpijNQIhQrs0EgFr4kIpIl4hPIzIsMF9unWAQSTfkyaCTKOd1ajDUdFeejHCI+NUEiA/Re9s/adCG63f2eMJzgle8QMCSI7LHuv3Q62ZWqngGIh5rEQCwuowQa1XuoQPweNlvznZ+pdRHBA8N7K7+gV3Kdq+JpXw9dSw2E/lHe+yVIjCxQRCY+IRIiADVHkFHygqVI7EBQWKQ+LVLAAsZjPzjZO6sCiAG2S/E5CIZ0ENHNt2XiaErFM6kAhoKJCxosKmUQF2A03o9xwoF1SIwoUEDkPiFyAgL1uHjp8iLgjtfNAUVHwqCiEioEz9vUMKoMGSC2jS3D+acl8sFfSjxf43Sy9wwwhFQB85oNYIj7sbKNmZNE8pth2JILpZ54tXggACXDI6q95lLHfdQimFXmORgEBBIHsC4D2RS3DS3BfIGLakoQBkIE5xQDoVtTBwL2/EMwwskiIhQTQbtIcQOghATQtaiSBzkexeFgLDyAPHjG2iDjWtAwgwM1DwoMgEQgeKwT9hkIwBcXCIhUsQCzmVFsBWhO1/J6AGch4DGTCALo6GGpKdNo9xzECACx1zpM6F6lhqZnzQ+pQPoaVL3jKF6I8OicPajvUIXVtFcTNh2dbEMVjgNtNOLM/6sBhjSWJWI8vLuXBRXj6JXKBYNiOqIOCBKbA51HgCwUXGIxAC6IOCFLseUUWBIFAAFuLXMpaBBoOdUBQ4N2D4tzuQSHdgwFwUNlExIKoA44MjhAhL0KEEiFACCb4o6qI91DL7wcsk8ib70IYABmY4sYSxG+opZGAGYh5DMTCwMAFYjnuQh0MLLG8IYuBtTAwcOq0HgYsvcMFPvasGkv1RFQfaCrDbYU6VA+wR9FYqqeiOuwgo+q65qHBEHvUiKV6JqrDnjGqlQd9g3pSgsjTRSwGcmEAdotRDIC+QT3JQeRZIhYDhTAAL+7Km9tQT24IFH750eUIX24uwvcL35cVRpxgetJByMNDLOF9Ef4xCZ9izwyxhA9EeED4SSsFxDH86RnkRx4XYjEQCgNwLtgkDH9uOw6MMpaPzDzIkjoSqdG0P8fwp0P5AptnkKV8LMrDyvdONWprruSDFnfuWd6A8+O+Z3eBAjCA9IYDRy8US/gpwDWv/q+l/sN2DpOyc8C2Px0U+DAFCY+CRCiA5w4iKQBtfzogCGAIUh4EqUAAm3ooQwfo+tPSHRy0MvNlfYS+3YWWflqIySQQG6AOWkI4YmS8iJFJxIAnlqIiBmgD1MFABDOQ8xjIhQEwOWw2ug5Wz6TFoA9QBwQxDEHBg6AQCEAI7CYEPTkD0AioA4I1DMHy44QDQbm5QNAPgUtZBCy9AwgJrLrPU90X1YdOKtZ5btDSPZiYwrIHPNkDkf18T5jm0cIMVj3kqR6K6rALjGznQSugnmQhCEHEgyASCGAbmHmuFVBP2hCZPJDFQCwMwMYgKvyDrkA9qSMXTh2xGFgLA6BHyPLOnitOT+YIhCDhQZAIBI8VggCGIOVBkAoEIARE5ghxC+rJBYAMZDwGMmFgaAq5Zxz4RPZJm4dRhv9B2XOe7LnIDstuU7LDLkIdFMQwBQWPgkIoGLj2VN/kYbbeyt/n9gMzAB4vA+AJBoMcJH0YOHoxWMO13+fJ7ovssBUEHxDCLIQ6IEhgCAIeBIFAAE8HREEAOgh1MJDCDIQ8BkJh4Hw/EOgg1MFAn7sPzBawmIiECXiKqGZ+uGeZe9AoqAOKDA4MMQ+CWCAYughhT8cQdApq+bWA5QtYEKwFAnjKKCJ5jDgFtTQPWL6ABUEiEIAQtJLHPYtRgk5BHRCU/j4wX8CCIBUIQAhaU4f2JI0sveMEPix7xpM9E9mHrj3ZU/c1jxIGsOw5T/ZcZD9/6jDNg4IhrHrBU70Q1c93iYFOQT3JQZCB5ccpLx8wFQYgl9jZTkE9qUGQAZ/HgC8MwAYhckVR0CqoJ0MEQhDwIAgEAhACt2eWGcQZpicrBAof8oQPRfjHJHwKCx/xhI9EeFB40iAOWgL1jPqDDMQ8BmJhYOAKMX3riJ3I3uoFeOOM84Oyr3myr0V2WHZy+TjYEqiDggKmIOFRkAgFMAUzigJbb+UvjXvg0D5L9lRkhy0gzcrfM5OYo1d2H5Y948meieznLgSGWQB1QBDAEOQ8CHKBAJ4KqAlBz7MAoAdQBwQhDEHBg6AQCIYuB9dj9QFNgDogiGAIlh9nvIH/mUAAQGDPKKsPaPrTAUEMQ+DzIPAFAng+KBdP9yOmPx0QrGEIAh4EgUAATw/V6BP0uH9Bz58OBhKYgZDHQCgMgAzMcAYQy58OBlKYgYjHQCQMgFYAk7FKsA7VM1j1mKd6LKrD1i+iH2jpHgTMYdnXPNnXIju6UCRa2TWPARaw6glP9URUHzgnWE8zDzr+9Az/T+HhfxYDqTAw0O3FcfzpyQWADGQ8BjJhAPb8UNEfNPzpSQWADOQ8BnJhAGSgmf3tYQC0gOnJBIAMFDwGCmHgkTIQwQwsP855iYC5MNDLgNfOBjFsgHryACADPo8BXxiA08LUSlEnqrdCwnScgX9Q9YCneiCqw6rj0R8zAeqAIIEhCHkQhALB0Hk/UA+gDtVTWPWIp3okqsOqU1Xf0at6Bqse81SPRXXY8+FRng/YA6iDghymYM2jYC0UwJP8NCnosX2DHkAdEBQwBAkPgkQggJ0/M8r5A3oAdUBQOvfAVAALglQgON/5A1oAdTDgwwxkPAYyYQCe6GlGMAA6AHUwEMAM5DwGcmFg4KxPHAegDgZCmIGCx0AhDIDWAAtnAHEA6mAgghlYfvwvy/wfXjZgv4eQ0E+CQyWFLL1jAzGsvc/W3hftMe09yhyieTRwDWsfsLUPRHvUHEbVe81jggmsfcjWPhTth68RyJkKUE9OACQhYpMQCQnUdFAoCaA9UE+eACQhZpMQCwkXmYNAk6CeXAFIwppNwlpIQC1C5ASRoE9MT8YARCFho5AICo8YhdLoB+YNuCikggKGgku1D6BxUE/2ACQhY5OQCQloMpHyEJ1o34JiNk7WANQ+Z2ufi/aMKSR6kgewi1AHCyHMQsFmoRAWGKaCntmlbL2BIILFL5MAFjttYIn4kPitJ4p7xHf0ih/D4vts8X0R/yInCWws1IHCGkYhYKMQCArDVw7rQQF0F+ogIYFJCNkkhEICOqmQS5AAWgx1kJDCJERsEiIhATUYUSYz0Giog4QMJiFmkxALCajNiIoJoN1QBwk5TMKaTcJaSEBtRs1+AmetYR0oFDAKCRuFRFBAJ6NqoND55Yh4D3WQcLALImkFHgypwIDB0FybhFh5WIf+Pqp/xtY/E/0x/Ym+oqV7DDFA5c/Z8uciP+Y6scnqr3kYMUT1L9j6F6I/pv/k7CkK9SQUMBjKnoLNzinYAgMEAzlfJWhG1JNgwGDw2TD4AsNFE1WBfkQ9KQYMhoANQyAwXGQ+Am1oerIMGAwhG4ZQYHi8MKQoDBEbhkhgwGCYnT2foZ5cAwZDzIYhFhjQFKRJzXh0ov9cS4YB03/N1n8t+g9f16ZvriPYnagDhwLFIWHjkAgOKA7k1Fe23nBw8BQiuQWe/qnoj/oQmuEAX/pYh/4+qn/G1j8T/dElrsyzbYo6aAhQGnI2DbnQgHpRKBpAp6IOGEIUhoINQyEwoOugUbZV0KyoA4YIhaHsRTjsvIMjMIDeJI/yJoGGRR00xCgNPpsGX2gYbk/ieBZ1wLBGYQjYMAQCA2pPojoNoGtRBwwJCkPIhiEUGFCvkom3E4hzUQcNKUpDxKYhEhouWlnR0ju4kKHyx2z5Y5Efk7/VaUSNi7pSDbD8a7b8a5Efk5+cOlPz0GKByp+w5U9Efkz+Od4vRHyLuvIMNppn4MGQCgyYB8Em0s6IcVFX1gGmIWPTkAkNGA0TqmUAjYu6kg4wDDkbhlxgQO1J1PyqoFdNV9IBhqFgw1AIDI8XhgiFoexSuOykgysw9MMwbWWgOMbFh4ThT6ss22Xt7mMFwZe3X1Z5F4TfLpJd/ruPFouF405PCIeXGA8vmUBY+/x0RcHLPseiVb56cKUrXQbofYHqoj2tvd2rPeBWHBMFJhAXYyFw0HB4vXDYGgLDUCZi1sCyaA1q3ewV1N2Chu7OmLr7mMr+ObXdlxpOqu40BpDq4cSG6oBVcRwI6Arvnx/+27sKFhAWbhMLpweLfs/imFQw2biYEOGE5KQ54rgfNmhz0m9nHJ8TmpY1h4y1UABS4HlktOi3MY5CQYBpHpwTFQKJBCQDzQfgejsS/e7FcRiga39wfivR3lWo6KfCbj0H09s+9NsYx6SCycbFhAgnJCfNPLbpdTixAIPj+JzQtCQcMhKhAKSgubxPTz/i3tk4iu4hpnJ4ThwIpe6Tqrd6j90BR2vcAceQruHh+S1Be1fhAOJgTtf+UQcgw6HxPry0d9B/ACEDepp+QO+g3/Q4Pic0LSmHjFQogNd9on5LQGbHUSiIMM2jQ6W2Odrf7yQMDJtmx5z2MNDvcRyHAbr2R+e3Eu1dhQpwfgW6B9nvbxuTCqUYwkXGISET7R+X9sy4cNj83Nhw2F0YGfZcfdfZADkex/S3qGYeS2SyPa/+k/O8PrTTod/odq91y/JmjaX8EP0Dtv6B6E/o7/KMjnpxGAJFyIYiFCgIKGaEwXF0CnJM8fyc3w25/GKg/U0uw+w4OgP+kNofsWt/JLWf5V5imR91QTEEjZiNRixoEJYmKhkBGyD1kjGEjzWbj7XwgfPRXDyQZXwcnY8CY6E4p0tRSJeCNsDNzjZBjk5EMCRKJOwokUiUIOxvdJSATJG6mBhCRsomIxUyCMObTaS0YWOkXjKG8JGx+ciED5YVbsYwRI4/cIWntnI2DbnQQFjkXDLJZekbrgiHxISCTUEhFOAUtHqYfeYHjQOX4fD2oZyPZcKewWUiLMBGGIuOCBoHMPsMjWR+k0eEL0TgRAzoMUAmyfFHrPAeQ8CmIRAacBqm1O8L2Cw5Og21Qcqhkp08JkJhgliUqi8DDhsmdXEwNPnFoyESGoilZ/pS37BZbvxRB7yNiNkExELA4yKgx9SIM7FmM7EWJohVZ/oWtR5klRz/RwYOQ8KGIREYCH9E//Rv95rb7R8UDx4ScM1TtuapaE5o3u+IA22SoyMQEw9SsBHIBAHa+4KaIkfXPKcfoMjPf7CqvauQAJLQHwwcfSSs6VwTr/bnUvsJZ5N3vilydBwSHIeCjUMhOBC2JnpuN8gIOToNKU5DmUTy2GknT2iAaZjPzrY9jk5DQXcaivM7De1dhREoTd1cnbInNQkbIUdnJMMjhs+OGL5EDMLoNiONbpAFcvyfGXRakkdDIDQQtra+dYgGuR7Hbz5wGEI2DKHAwJn4rW+sGbI4jg7Dkk5H8mCIBIaLzW2WvmEHn37gjqd/LPoThjZyjg6N448B/TwdT/61yI/L79DVX+OoY0g/KcXTPxH9cf3pvgBkXtSQgyQfjuLBkAoMOAxzEgbIu6ghG0k+CcWDIRMYcEdKcwChDwbIwKghOYXCkLNhyAUGHAaPGluE7WsaclPkA1E8Ggqh4fHSkNKPRE3Zuamp0ADTMCcbCsi6qCHtQD4NxYPBFxjo5ahQ66LT7kE+fHKBnOGRp3kgmhOaM2d4HB2Bgp7PkYdAKAjQk/Cg1sXxq/3QGaDz3qcdOD8WZBURnneFM+fj6Jws8ccfI3ZsiCQ2EJMx0WvVgsbG0XHwcRxiNg6x4HCxTQkyNo5OQ4DTsGbTsBYaCJuSS9qUIGPj+N3IoV2K4tIuRf8BhBqIGjJrCVsdR6cmxGNIwo4hicQQnIYJ8ews7HQcHYYIhyFlw5AKDDgMU8LPAjsdR4chxmHI2DBkAgNnaVOO03F0GNY4DDkbhlxg4Ezd1geDpW8YIsHlL9jyFyI/x+mGGx1Hlz/F5S9zjjN2lnIm8iNGN7L2axyEzHD5fbb8vshPWNvIngDkc9SQsERhCNgwBAIDYW0jYYB8jhpSl+TsjDwYQoGBWKSUNzujhgSVSyWoeAREQgBOQG/yGrawachJoQTEbAJiIeBxERDgBKzZBKyFAIyASSsPxTExakgooDAkbBgSgYFIUZuEidFtB4aHzxugmqdszVPRnLYlcEyMoyMQ4whkbAQyQYBAoH/aVVtfte+xFlJJAh4DuTBArw+HGhRHZ2CN1/uCrXkhmhNuEpN0k4AGxdFxSHAcynH/OTtTMBcckLmSaBwgg+LoNKQ4DT6bBl9oIMxFpJ8E8ieODkOPa5BKJPDgCASOy2bSgm2Io8OR4ZEiZMMQCgzETFpkpIBsiOP/rqBzCjwYIoEBzzebjU6E1Td9M+RDHL/doPMLPBpioQGnwW7S0JdrgIyIo9Ow/Dihcg08GtZCA2fFUNyIOLr8Pi5/wpY/EflZU651n4e0dA45Brj+KVv/VPS/1IqmcbQxxOXP2PJnIj9hPqP7ApAVUUPaEaUhZ9OQCw2E+8w814qoIQGJwlCwYSgEBsKGRLYMkCtRQ1YKhWH58b9sk5uGKPcQGCBHkuWdPcmehqQUSoPPpsEXGh4vDSlOQ8CmIRAacBqopBTsVtSQd0BhCNkwhAIDK1/dN9R8r/+kzcXDpxpQ/SO2/pHoT+hvk/qDLsbRcShwHGI2DrHgwFnqq3e6NVtfOFh+9IjsAlP/tejPMaz06u/o09/H9U/Y+ieiP+FJIUaUEDPj6DQEOA0pm4ZUaCCmQyJpgLyMo8MQ4jBkbBgygeFShxLkZRwdhgiHIWfDkAsMxNxYzTS0zTAvjk5DjNNQsGkohAbWMpB9vUbIvTg6DWuchjKTYLFzD5bQgMyVReWoYffi6DQkOA0+mwZfaMBpaOWo+9YIhdyLo9OQ4jQEbBoCoQGnoTXBal8mytI3vpDh+ods/UPRn7VIaF800Di+mOP6R2z9I9H/0snTNA4vFrj8MVv+WOS/1LAGuRc15BqmVK6BB8NaYCAMa2e7FzUkHlAYEjYMicBAWJToVWEh+6KGxANKQ8qmIRUacBrcvsl0YJOahmwDSkDGJiATAh4XARFOQM4mIBcCcAJoPztkU9SQYUBhKNgwFAIDZ2Ge3pXe7vVvdRS8EXIKqP5lhsBm5xRs0R/Rn17pD7Qpjo5DguPgs3HwBQcChxmJg60vHKS4/gFb/0D0J7wozXDQN8uao0//DNc/ZOsfiv6XLc2G2BRHpyHHaYjYNERCAzFdUpOGvmcYIJ/i6DQUOA0xm4ZYaGCt1NdnRoKMiqPTsPw4o5IMPBrWQgMxedaMNCNBRsXRafBxGhI2DYnQQEye5RL2A9ioODoNAU5DyqYhFRqIubQa/YY+DzPkUxwdhhCHIWPDkAkMOAwzAgbYpjg6DBEOQ86GIRcYcGuCyVjteXT5Y1z+gi1/IfITLjWq02jpHF5c4/qXuQOHnW1wRH98VU+8+mscXUxw+X22/L7Iz5lJra8rALkUNaQaUBgCNgyBwMAxpnFcihryDigMIRuGUGAgXElkwwCZFDWkHVAYIjYMkcCAw9BMQvfBALnVNGQdUBhiNgyxwPBoYVh+nFNJBx4Ma4EBg8Frp6AY1kUNOQcUhoQNQyIwENlpcpmve/lbMWI6QpIBlT9ly5+K/IT8RMOAGBdHpyHEacjYNGRCA2umFNS3OLr8ES5/zpY/F/kJ+clg4OiTP8blL9jyFyI/YUbxSDMK6FscHYc1jkOZNHDZaQZXcEAmSmri0Odih3yLo9OQ4DT4bBp8oYHwJs1IbxLkWxydhhSnIWDTEAgNl3qTINvi6DBkOAwhG4ZQYCBmzZpRMECuxdFhyHEYIjYMkcDAmUKL41ocHYYChyFmwxALDLhVwSJggF2Lo8Oguv+W+T9U5oHHw1p4wHlwyDSUpW+AwScJSNgEJEIAToBH+lU0jjAGJAEpm4BUCCDsa2QM0DjIGJIEZGwCMiGAs94jZ5pFDTkHioeczUMuPNCTaeE8QB5GDUkIioeCzUMhPFxqVoJsjBqyEBQPZVphwk5ETIQHxK9ET74Judc0JCIoIHw2EL4A8XiBSEkgAjYQgQCBA+GSLQbkaNSQjqB4CNk8hMIDkawkfUz3BLTImI2Qg6AIiNgEREIAayqNvjwEaGwcnYiCJCJmExELESwDQ980XLa+oFCmHywy/cBDYC0IEIt9uSQCjj4EfBKBhI1AIghcalwBLY6jAxGQQKRsIFIBgrPkWx8QkMlxdB5CkoeMzUMmPBATLbkUD5DNcXQeIpKHnM1DLjwQfibS3AY5HUfnISZ5KNg8FMIDYWki4wNkdhydhzXJQ5lq8NjJCU94QCxNzf4DZznp0YFISCB8NhC+AEHMztUAovsbE/Y8js5DSvIQsHkIhAech+baMMSa0qMjkJEIhGwEQkEAR4DqQ1o6Rx5zkoCITUAkBOCWFpsOAhpHHgsSgZiNQCwI4AhMzp62UUsywiaTETwe1sIDZwHJPh4g16OWzATOQ8LmIREeLp2VC3I9aklM4DykbB5S4eFSTxPkcdOSmMB5yNg8ZMLDo+UhInnI2TzkwgPOw+zsWRy1JCZwHgo2D4XwQCQuTXL2pnsE5jpyETgCZWZhys5FTAWBoYsE9c7YBJoeRyciIYnw2UT4QgRBBD2Hl60vKKQkAgEbgUAQIAwMzaCAL0Y9OgIZiUDIRiAUBIj1wsyzTY+jA5GTQERsICIBgjCxkEBApsfReShIHmI2D7HwQKwoR5pgIdPj6DyUuQmHzE3weFgLD4SpySNNTZDrcXQgfBKIhA1EIkBwTE0c1+PoPAQkDymbh1R4IExNZAcCMj2OzkNI8pCxeciEB8LhZBINBux6HB2IiAQiZwORCxCXrktp6Rt0iEkCCjYBhRCAE9DqQ6KmRy3pCJyAMrkwY6cjZkIATAA916fGgceEJMBnE+ALATgBc6KbCHseteQicB4CNg+B8IB7FmwqRw2bHrVkJnAgQjYQoQCBAzEhmwjI9KglMYHzELF5iIQHwtRETgULmdy0JCZwHmI2D7Hw8Gh5KBMTLpmY4PGwFh4wHqatRBXH9PiQPPySLbb5ZlEE7ZGm3y6SXf676t+KjLtuq3G6UfXvR5vViPQe4AkxgyFz4cjkgZhTYFpgHJwPJZqT0Rk5qGdBrCTsCJI8uQjygDS0hyXrmYMH4dByTlpjwJGqigygkLJRSAWF4eOTnMBgt8csRiAh+OhCJGRsEjIhYfg4JSsoOO3RilGCwgRCIWejkAsKwwcsOUHBbf8OGaPv8HEKkVCwSSiEBMZQJYOESfsXyAgkLOulLLsklGmpOTuRNRcSWGOUg0jw2l+M0jrczyXehcFnw+ALDOwBqUEwPORKE3ADcW+e7sIQsGEIBAb2aNQgGB7yEVy4jbgfoOzCELJhCAUGDAbv7A7D+A643hFDIrPFgyN6cnCM6pDsG7nu5+PScUjIDFP2/YlcFo+AWAg4Z+xxEAIPOfYIuWEIINZsINYCxBkjkIN4eMgRSMgMQ/CQsHlIhIdzxiEHAfGQ45CQG4YAImUDkQoQZ4xGDuLhIUcjITcMwUPG5iETHs4YkxzEw0OOSUJumFI74iEbHg+58HCpexLi4SFHJqGndAkeCjYPhfBwqVsO4mH0ZXADkgcVQRyTm7co9xAeznfLQTzomEKU4MFn8+ALD2cMUQ7i4bIhyqZoyW61LY56vO3qVUl0jPqleqhe9mRyvmKL7UqV2mq3VTcRJKUohrqNwN+/qi5YvUjU4VbbqIHPcrfL/Nz4chjl/VqPGZ/osb/VD6u/H07pnH66L7j7KxlaXu+eQHnZD1xezXjzIYjKz1sB520Va9514swCDzH54Wh18S5+1fjSZc4+lOFL+/qSGNSqyavbZLNaropjaW1KOf+4LYIsV/es5M+r6zq53XUQJL+oQ//bdp+RCnfZbbVNTSSziTgotugo9vZgsEZ1a0WZwy6/bt0ZL2IML87+xvbt0YnML1S107dWrC81lus7rFzf8VF9942hao9bpkC0bjrjT4qxGbuHFG8ngkMF/E3E8ccVxjGQv39CPZWXtoau3Q9PqMAeqryGBIvvqyDxQyc83PACw803EhJeuodCNA+FOHsyMeH9E0C8HbHHDAk/PqHyerAYOiQmvK9iwo+dmLDixYTVNxIT2iHhpflkYsIfngDj5YzJDX3GDAo/PYECsx+4vIbEhD9UMeGnTkz4Gy8m/O0biQl1YHWYMcH5RoKCKvBtrr7YH6t8HwW7KLjJFr//f1BLBwj1Wq9XwCsAAMS5AwBQSwECFAAUAAgACACvAYk/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAK8BiT/1Wq9XwCsAAMS5AwAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAVywAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="727" height="439" version="4.0" ggbBase64="UEsDBBQACAAIAK8BiT8AAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAK8BiT8AAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s7Z3pkhvJccc/y0/RMR8UdgQ57AsNYEXKQe5ytQqvbIW4Vjj8hYFBXxAwQF/DQ7bfxm/iF3M1Go1BH5nZCUzXcmZSoeXg6LP+v8oqVP676vU/f7ndGJ+CLF/ttm+urGvzygi2y52/2kZvru6K8OXs6p9//w+vo2AXBTfZwgh32e2ieHPllluu/DdXM2c6syaO/3LpqH/cm8XNy9nUtl9as9ncWcxuPG8+uzKML/nqu+3uXxe3QZ4slsGHZRzcLn7eLRfF/sRxUSTfvXr1+fPn6/pU17ssehVFN9dfcv/KUJe5zd9cHV58pw7X2Omzs9/cNk3r1X/86efq8C9X27xYbJfBlVHewt3q9//wm9efV1t/99n4vPKL+M3V1HWujDhYRbG6p8nUuzJelRslqkCSYFmsPgW52vXk7f6ei9vkar/ZYlt+/5vqlbE53s6V4a8+rfwgK4t0MlMF5Fm2M7Ntx7VUaeyyVbAtDttah3O+qo/2+tMq+Fwdtny1P6Pa6NMqX91sgjdX4WKTq1tabcNMFefxfV583QQ3i+z4wf3lqHvMV39Xm1rWTMlWFYF6Z5ovyv889Z9rmtV1nJzUvTKK3W6zP6Zp/Pd/G7Zpm8aL8o9V/bHVH8+rvjKrz0yn+mNXf9zqz6Taxq12d6tN3Wobt9qmVOJ4j0V2h95i9f39HVr1HU7t6fAbtB+oVM2eQrUn/ee0POSk1W0h5zzepzU5Oac61f7/+/86Z3Sw22yfESxYxgk9V8stvn5VV5TXB0yNPC63PcBTBLd5Ca4zNybzkj/LmChIvanCbWJYc/VnahsKS8OaGO5EvbVmhlf+nRrOVH3hGo4xM8rtLMfYUzqZqX/c6f5gnjFRBys/narKYVjqRK4xcQxrD7drKKSNfQVRlcV21BaTiTFRO5Wnt+zyEI5nuJ5658wMV11jWTemltrQUTuq9+r0tuFYhlPubE0N2zO88niWW9Y5b1ZeujqkbXim4VnlAVX1UlWrqlZq+5nhlHdTB7XVNrkrGkW0vPXrl8UuOWqhtlbR6D7mVdGpERJ/83qzuAk2qpX4UCppGJ8Wm7JG7E8U7raFUYtoV59F2SKJV8v8Q1AUaq/c+Nvi0+LnRRF8+VFtndfn3m+73G3zP2e74vvd5u52mxvGcrcxj9e821gnr+3jVas3zskX7ukXk5MvvJPX097z7tQ3xl0eqPPvsrzefOH7fyy3uA8NqiT/bbv5+i4LFutkt2rexutX+wbndXC33Kz81WL7VwVreZayXIy6/akCct0AzdxJfSW7zP/wNVcIG1/+M8h2ZVzxrudT1dqanj2ZW7aqJl+rb2zPvjbntu1OzanlOXN1ZcvFZh/tJ9fWZOY686k7tc3ZXNXLr8B302l15uDTUaHFl+B481FWVuzDjZdv/pi/223uP9rf/veLpLjL9j0HFRuz8p7ebqNNsEdkH21Vs7xc3+y+fKjYcKpj/fI1Ue/M6gJuon2xGyo02JOJ2uDw96b6u9+mvLLjVuZ+G3O/hVnDtvKP31tze7/F/u9N9Xe/laK3urTDnVr1bVpmfZpVvg9o5lWj2uzRLxv5u+2q+Ll+U6yW68OdWtX2/3p3exMcAWoe0nqgQ75+1QLsdZ4oHv08DoKiF7l9C1kT51pWdWFqp/D7YLP50Nj0hE37UGonh6/qZ307h30mM2w7+7idZVrYhs79hlMT29A92XCObTg5bujUlxhsyoC22xpG/GGZ7TabvdSfTl4v9/vvX2alWodL2Sy+7u7KGKck+VH1iO82i3f3rWf56R/2JN2//6k6aGurv/Z++k6dKg+yP6v+4KYRbaq7+UndXNDY4S/q+PsPjWOw2mx2nz+oeL1abN77q2J339Luv/pFNZi/rJJj/Q7SO/XtX9SfVRb4jah4WpoKkB/3PwCMww+BPy1Us2G+MF/cvLAm3zkvvOqF+8KuXqg+UPXCqr+y6xfmi5fWi8UL87uyv1R/Z9dbH15M6o2c+hP3fn+rfjGpTz+vt5nVu1vl7tWuL5YvXtoTT20/rU83r083rw/l1J/M6m1m9cFn9cGPG1tWvZFbf3QsAKvezayP6NYbH27Jql/YxwJw61uxTsrkeIBjKbv1i2Ph3B/g/pjHI9VfHaWY1IeeHK/WrG/gWMzHsx3vZFJvM68/mR73txpF7N6X47Gsp/VOTv2JdX+Jx4I87ufUJzuWf+cc1RGrKNiJeq/XQabqz6FdVy3a3e4ur7opJ3D7qobcqrfVF4cQtygbrX9Xgbj61A+iLKjj92b/27RqNvbfmqctdufj/aF+zHa3f9x++kW1iK0LeP2qvsrX+TJbJWXDa9yovvD6vhKqn5L5QnWlT2vlvquiam4VvYpVUTYRqmrfFXFZ09U+qmel/pb9jy+qZPLy533dyHyvgrX69M3Vb9O7XfG7vyz8lSqZ1da4rT7Yn0CFxlv1G9Uo9m2z6qYVVyf77+OCCjzG7uZvKoTe9+KrLU4KWG0AtNQqECXxQr26vg+qKoKdlt7+cH/a+adlqhq86tJ67+2H5r39+22oFDAC1dLnxr9kwSoPOHf6wzd8p++bd/ov5aeb//vfbaS6M3ehUTYGPy/Um+F3+/4bvtu3duNuyzsbdlNqx2/lphoXub27DbLV8ngV76rrVLveHQ5g1ad6uGu3Bl67VQcvFRv3EUb9EEmqPmgSBFV3rzh02o1EHW7f5z+5mMXdl9Vmtci+Vsc76awOLI7v+4pj8nzL44dOeXjXzvMtjvddPGzvideXbkx0zo2JziOJiU5bZfuJa4zHxE5xWNfWc46JnfLwrufPtzjed/FwZk+8vnRjontuTHQfSUx02yo7T1xjPCZ2isO6tp9zTOyUx/T6GRfH+y4eE/OJ15duTJycGxMnjyQmTtoqu09cYzwmdorDunaecRD4oVMes/rqn2NxvO/i4T3131XdmOidGxO9RxITvbbKkyeuMR4TO8VhXbvPOSZ2ymN2PX2+xfG+i8f0qfchujFxem5MnD6SmDjtDhg9bY3xmNgpDut68pxjYqc85s86x9LFY/bU60s3Js7OjYmzRxITZ90Bo6etMR4TO8VhXXvPOSZ2ymP+rHMsXTzmzy/HMj83Js4fSUycd38cPW2N8ZjYKQ7revqcY2K3PMxnnWTplIdtPb8ki2WeGxXVno8jLB4utNEZeNoy43GxWx7W9ewZB4IfegrEetaplm6B2Pbzy7VY1tmh8duxpBOh0erpEzxtnYnY2C2Q6/mzjo3dArGedcqlWyC28+xyLj9YzQdb/hDki9uieo5n6DNKIz3hgjyIfb/18ZHsh46o762uxX9mPvWY2uHjxxYfAx/l+nEsKB7mGb2mSbd6Ls9Ist3+ibXvhnL/SBy7P1gdw439xDle7m5vF1vf2O5nfPl+lS03wb4MqilIFuabq39URTB5YZRPdf2TugtrL8AhluzuinqzZXXowwE7Zb3cbU9KetkFojG7wpg8nE4nUcSr5XqroN/Pd3AszPLFTyvfD7ZHFYJVFGw/qSvdZblhfDHfVDNwfTWr8xt/rz/5ogro5f6jr9bho78fXuwPpLTMVl+Mt/X2b+ut3trlC8u0VeR+6xwO+9atjlZ+NlEv75+tC9JtdQ95Ne1EOeXLKlwtcYX/ur+DjsIvDPOgrVLb2r9r63uH61sVzVHAu1+zxh+e8c6NL1V1M77WIp0e6gwITh4dP5T6cpEVQb5abA9BolDv/1zOsGJUJzcbJz9AAMvzS7bY5ptF0a6Dy0qcu26t++0i2eW/Y9W9wy5SA4EaaPfVQGtiNv5nP1CFBBU/qITrfrb6wgDOgNfHgP1QUZgQnSH9hQAIBigGtgoFJ3Xe6iLhaEUCB8PnYOCL6IDojtkQ3e6K7rrzxv+8kRnwQcX51d+XKo+q7zbVd7rqT1rqjy0+UenPbQd8aQEG4DBptgBuFwfvV8GBAcWFaAggKCCeR8WL6a8ICI5JwIEiEAQABGY21WGY6UUgAAXnx4JA6j8ivn1tmlQDMW+KPxtbfKLOn9soBNIcDMDBbuLgtXFQm/4qODCguBANAQQFxLXx/sJ+oiiNSOBghBwMQhEdEL3VSewMLVrjDy2GoMT8+h5KHUflnpN1fPRhw5Co1+eG+lCCPAmAM6AX4DbTSWNnk8JBwf6yXkDf7gJIPyAT4ldD+Xh3AxBHJyA4JhEHikgQABBojRpMuwh4TQTckRGIQMH5sSCS+o+I7+7zy3iHcPptif/ROkP+jz3PBAgA3ygARNA/t1cQSX9gAA7NNFPHZ1A+rNagQaMdUL2+trp2wE84BC074Kdvxw5oHhx51uO3A37qqHJwi3y0OVX0fiepnoAlpNcSeFILW+5Aa4wI3XAEgtJfAIBgQGHg8pyhGqlgsHExIcIJxcmMcI9qBwPHI+egkIvskHXMZbhFdSDgQ4L758QAX+o9zyzGco5q4QEPA/757UN7VyGknxCPyAwh7lKNgDAwuRgWQYZAZuqe7UDVjgwOTsGBpBAgILvh7GzHqQ4gAkj+4JxYEUh8oAyIZHwA3adacMBjQnB+M9LeVQDpB6T1EFvHjIA4VDUCwsDkYlgEGZ5JccZwsWpHhhj54iUul5KyhE2MLpWytPQOb4SQ6OE5ESKUqEAA0Op49jhWNA9xhnjdD89vLtq7ChJ9SDjXFhkTNA959hgdCTAuxkMgISChexOgG1Y7MsTQF6834UtvAoRiSvwqQRywOqCIIARqa5vDAeF+J8GhDwd3P4rBcMBqQQCPBdH5zUd7V4GiH4q+PDpijNQIhQrs0EgFr4kIpIl4hPIzIsMF9unWAQSTfkyaCTKOd1ajDUdFeejHCI+NUEiA/Re9s/adCG63f2eMJzgle8QMCSI7LHuv3Q62ZWqngGIh5rEQCwuowQa1XuoQPweNlvznZ+pdRHBA8N7K7+gV3Kdq+JpXw9dSw2E/lHe+yVIjCxQRCY+IRIiADVHkFHygqVI7EBQWKQ+LVLAAsZjPzjZO6sCiAG2S/E5CIZ0ENHNt2XiaErFM6kAhoKJCxosKmUQF2A03o9xwoF1SIwoUEDkPiFyAgL1uHjp8iLgjtfNAUVHwqCiEioEz9vUMKoMGSC2jS3D+acl8sFfSjxf43Sy9wwwhFQB85oNYIj7sbKNmZNE8pth2JILpZ54tXggACXDI6q95lLHfdQimFXmORgEBBIHsC4D2RS3DS3BfIGLakoQBkIE5xQDoVtTBwL2/EMwwskiIhQTQbtIcQOghATQtaiSBzkexeFgLDyAPHjG2iDjWtAwgwM1DwoMgEQgeKwT9hkIwBcXCIhUsQCzmVFsBWhO1/J6AGch4DGTCALo6GGpKdNo9xzECACx1zpM6F6lhqZnzQ+pQPoaVL3jKF6I8OicPajvUIXVtFcTNh2dbEMVjgNtNOLM/6sBhjSWJWI8vLuXBRXj6JXKBYNiOqIOCBKbA51HgCwUXGIxAC6IOCFLseUUWBIFAAFuLXMpaBBoOdUBQ4N2D4tzuQSHdgwFwUNlExIKoA44MjhAhL0KEEiFACCb4o6qI91DL7wcsk8ib70IYABmY4sYSxG+opZGAGYh5DMTCwMAFYjnuQh0MLLG8IYuBtTAwcOq0HgYsvcMFPvasGkv1RFQfaCrDbYU6VA+wR9FYqqeiOuwgo+q65qHBEHvUiKV6JqrDnjGqlQd9g3pSgsjTRSwGcmEAdotRDIC+QT3JQeRZIhYDhTAAL+7Km9tQT24IFH750eUIX24uwvcL35cVRpxgetJByMNDLOF9Ef4xCZ9izwyxhA9EeED4SSsFxDH86RnkRx4XYjEQCgNwLtgkDH9uOw6MMpaPzDzIkjoSqdG0P8fwp0P5AptnkKV8LMrDyvdONWprruSDFnfuWd6A8+O+Z3eBAjCA9IYDRy8US/gpwDWv/q+l/sN2DpOyc8C2Px0U+DAFCY+CRCiA5w4iKQBtfzogCGAIUh4EqUAAm3ooQwfo+tPSHRy0MvNlfYS+3YWWflqIySQQG6AOWkI4YmS8iJFJxIAnlqIiBmgD1MFABDOQ8xjIhQEwOWw2ug5Wz6TFoA9QBwQxDEHBg6AQCEAI7CYEPTkD0AioA4I1DMHy44QDQbm5QNAPgUtZBCy9AwgJrLrPU90X1YdOKtZ5btDSPZiYwrIHPNkDkf18T5jm0cIMVj3kqR6K6rALjGznQSugnmQhCEHEgyASCGAbmHmuFVBP2hCZPJDFQCwMwMYgKvyDrkA9qSMXTh2xGFgLA6BHyPLOnitOT+YIhCDhQZAIBI8VggCGIOVBkAoEIARE5ghxC+rJBYAMZDwGMmFgaAq5Zxz4RPZJm4dRhv9B2XOe7LnIDstuU7LDLkIdFMQwBQWPgkIoGLj2VN/kYbbeyt/n9gMzAB4vA+AJBoMcJH0YOHoxWMO13+fJ7ovssBUEHxDCLIQ6IEhgCAIeBIFAAE8HREEAOgh1MJDCDIQ8BkJh4Hw/EOgg1MFAn7sPzBawmIiECXiKqGZ+uGeZe9AoqAOKDA4MMQ+CWCAYughhT8cQdApq+bWA5QtYEKwFAnjKKCJ5jDgFtTQPWL6ABUEiEIAQtJLHPYtRgk5BHRCU/j4wX8CCIBUIQAhaU4f2JI0sveMEPix7xpM9E9mHrj3ZU/c1jxIGsOw5T/ZcZD9/6jDNg4IhrHrBU70Q1c93iYFOQT3JQZCB5ccpLx8wFQYgl9jZTkE9qUGQAZ/HgC8MwAYhckVR0CqoJ0MEQhDwIAgEAhACt2eWGcQZpicrBAof8oQPRfjHJHwKCx/xhI9EeFB40iAOWgL1jPqDDMQ8BmJhYOAKMX3riJ3I3uoFeOOM84Oyr3myr0V2WHZy+TjYEqiDggKmIOFRkAgFMAUzigJbb+UvjXvg0D5L9lRkhy0gzcrfM5OYo1d2H5Y948meieznLgSGWQB1QBDAEOQ8CHKBAJ4KqAlBz7MAoAdQBwQhDEHBg6AQCIYuB9dj9QFNgDogiGAIlh9nvIH/mUAAQGDPKKsPaPrTAUEMQ+DzIPAFAng+KBdP9yOmPx0QrGEIAh4EgUAATw/V6BP0uH9Bz58OBhKYgZDHQCgMgAzMcAYQy58OBlKYgYjHQCQMgFYAk7FKsA7VM1j1mKd6LKrD1i+iH2jpHgTMYdnXPNnXIju6UCRa2TWPARaw6glP9URUHzgnWE8zDzr+9Az/T+HhfxYDqTAw0O3FcfzpyQWADGQ8BjJhAPb8UNEfNPzpSQWADOQ8BnJhAGSgmf3tYQC0gOnJBIAMFDwGCmHgkTIQwQwsP855iYC5MNDLgNfOBjFsgHryACADPo8BXxiA08LUSlEnqrdCwnScgX9Q9YCneiCqw6rj0R8zAeqAIIEhCHkQhALB0Hk/UA+gDtVTWPWIp3okqsOqU1Xf0at6Bqse81SPRXXY8+FRng/YA6iDghymYM2jYC0UwJP8NCnosX2DHkAdEBQwBAkPgkQggJ0/M8r5A3oAdUBQOvfAVAALglQgON/5A1oAdTDgwwxkPAYyYQCe6GlGMAA6AHUwEMAM5DwGcmFg4KxPHAegDgZCmIGCx0AhDIDWAAtnAHEA6mAgghlYfvwvy/wfXjZgv4eQ0E+CQyWFLL1jAzGsvc/W3hftMe09yhyieTRwDWsfsLUPRHvUHEbVe81jggmsfcjWPhTth68RyJkKUE9OACQhYpMQCQnUdFAoCaA9UE+eACQhZpMQCwkXmYNAk6CeXAFIwppNwlpIQC1C5ASRoE9MT8YARCFho5AICo8YhdLoB+YNuCikggKGgku1D6BxUE/2ACQhY5OQCQloMpHyEJ1o34JiNk7WANQ+Z2ufi/aMKSR6kgewi1AHCyHMQsFmoRAWGKaCntmlbL2BIILFL5MAFjttYIn4kPitJ4p7xHf0ih/D4vts8X0R/yInCWws1IHCGkYhYKMQCArDVw7rQQF0F+ogIYFJCNkkhEICOqmQS5AAWgx1kJDCJERsEiIhATUYUSYz0Giog4QMJiFmkxALCajNiIoJoN1QBwk5TMKaTcJaSEBtRs1+AmetYR0oFDAKCRuFRFBAJ6NqoND55Yh4D3WQcLALImkFHgypwIDB0FybhFh5WIf+Pqp/xtY/E/0x/Ym+oqV7DDFA5c/Z8uciP+Y6scnqr3kYMUT1L9j6F6I/pv/k7CkK9SQUMBjKnoLNzinYAgMEAzlfJWhG1JNgwGDw2TD4AsNFE1WBfkQ9KQYMhoANQyAwXGQ+Am1oerIMGAwhG4ZQYHi8MKQoDBEbhkhgwGCYnT2foZ5cAwZDzIYhFhjQFKRJzXh0ov9cS4YB03/N1n8t+g9f16ZvriPYnagDhwLFIWHjkAgOKA7k1Fe23nBw8BQiuQWe/qnoj/oQmuEAX/pYh/4+qn/G1j8T/dElrsyzbYo6aAhQGnI2DbnQgHpRKBpAp6IOGEIUhoINQyEwoOugUbZV0KyoA4YIhaHsRTjsvIMjMIDeJI/yJoGGRR00xCgNPpsGX2gYbk/ieBZ1wLBGYQjYMAQCA2pPojoNoGtRBwwJCkPIhiEUGFCvkom3E4hzUQcNKUpDxKYhEhouWlnR0ju4kKHyx2z5Y5Efk7/VaUSNi7pSDbD8a7b8a5Efk5+cOlPz0GKByp+w5U9Efkz+Od4vRHyLuvIMNppn4MGQCgyYB8Em0s6IcVFX1gGmIWPTkAkNGA0TqmUAjYu6kg4wDDkbhlxgQO1J1PyqoFdNV9IBhqFgw1AIDI8XhgiFoexSuOykgysw9MMwbWWgOMbFh4ThT6ss22Xt7mMFwZe3X1Z5F4TfLpJd/ruPFouF405PCIeXGA8vmUBY+/x0RcHLPseiVb56cKUrXQbofYHqoj2tvd2rPeBWHBMFJhAXYyFw0HB4vXDYGgLDUCZi1sCyaA1q3ewV1N2Chu7OmLr7mMr+ObXdlxpOqu40BpDq4cSG6oBVcRwI6Arvnx/+27sKFhAWbhMLpweLfs/imFQw2biYEOGE5KQ54rgfNmhz0m9nHJ8TmpY1h4y1UABS4HlktOi3MY5CQYBpHpwTFQKJBCQDzQfgejsS/e7FcRiga39wfivR3lWo6KfCbj0H09s+9NsYx6SCycbFhAgnJCfNPLbpdTixAIPj+JzQtCQcMhKhAKSgubxPTz/i3tk4iu4hpnJ4ThwIpe6Tqrd6j90BR2vcAceQruHh+S1Be1fhAOJgTtf+UQcgw6HxPry0d9B/ACEDepp+QO+g3/Q4Pic0LSmHjFQogNd9on5LQGbHUSiIMM2jQ6W2Odrf7yQMDJtmx5z2MNDvcRyHAbr2R+e3Eu1dhQpwfgW6B9nvbxuTCqUYwkXGISET7R+X9sy4cNj83Nhw2F0YGfZcfdfZADkex/S3qGYeS2SyPa/+k/O8PrTTod/odq91y/JmjaX8EP0Dtv6B6E/o7/KMjnpxGAJFyIYiFCgIKGaEwXF0CnJM8fyc3w25/GKg/U0uw+w4OgP+kNofsWt/JLWf5V5imR91QTEEjZiNRixoEJYmKhkBGyD1kjGEjzWbj7XwgfPRXDyQZXwcnY8CY6E4p0tRSJeCNsDNzjZBjk5EMCRKJOwokUiUIOxvdJSATJG6mBhCRsomIxUyCMObTaS0YWOkXjKG8JGx+ciED5YVbsYwRI4/cIWntnI2DbnQQFjkXDLJZekbrgiHxISCTUEhFOAUtHqYfeYHjQOX4fD2oZyPZcKewWUiLMBGGIuOCBoHMPsMjWR+k0eEL0TgRAzoMUAmyfFHrPAeQ8CmIRAacBqm1O8L2Cw5Og21Qcqhkp08JkJhgliUqi8DDhsmdXEwNPnFoyESGoilZ/pS37BZbvxRB7yNiNkExELA4yKgx9SIM7FmM7EWJohVZ/oWtR5klRz/RwYOQ8KGIREYCH9E//Rv95rb7R8UDx4ScM1TtuapaE5o3u+IA22SoyMQEw9SsBHIBAHa+4KaIkfXPKcfoMjPf7CqvauQAJLQHwwcfSSs6VwTr/bnUvsJZ5N3vilydBwSHIeCjUMhOBC2JnpuN8gIOToNKU5DmUTy2GknT2iAaZjPzrY9jk5DQXcaivM7De1dhREoTd1cnbInNQkbIUdnJMMjhs+OGL5EDMLoNiONbpAFcvyfGXRakkdDIDQQtra+dYgGuR7Hbz5wGEI2DKHAwJn4rW+sGbI4jg7Dkk5H8mCIBIaLzW2WvmEHn37gjqd/LPoThjZyjg6N448B/TwdT/61yI/L79DVX+OoY0g/KcXTPxH9cf3pvgBkXtSQgyQfjuLBkAoMOAxzEgbIu6ghG0k+CcWDIRMYcEdKcwChDwbIwKghOYXCkLNhyAUGHAaPGluE7WsaclPkA1E8Ggqh4fHSkNKPRE3Zuamp0ADTMCcbCsi6qCHtQD4NxYPBFxjo5ahQ66LT7kE+fHKBnOGRp3kgmhOaM2d4HB2Bgp7PkYdAKAjQk/Cg1sXxq/3QGaDz3qcdOD8WZBURnneFM+fj6Jws8ccfI3ZsiCQ2EJMx0WvVgsbG0XHwcRxiNg6x4HCxTQkyNo5OQ4DTsGbTsBYaCJuSS9qUIGPj+N3IoV2K4tIuRf8BhBqIGjJrCVsdR6cmxGNIwo4hicQQnIYJ8ews7HQcHYYIhyFlw5AKDDgMU8LPAjsdR4chxmHI2DBkAgNnaVOO03F0GNY4DDkbhlxg4Ezd1geDpW8YIsHlL9jyFyI/x+mGGx1Hlz/F5S9zjjN2lnIm8iNGN7L2axyEzHD5fbb8vshPWNvIngDkc9SQsERhCNgwBAIDYW0jYYB8jhpSl+TsjDwYQoGBWKSUNzujhgSVSyWoeAREQgBOQG/yGrawachJoQTEbAJiIeBxERDgBKzZBKyFAIyASSsPxTExakgooDAkbBgSgYFIUZuEidFtB4aHzxugmqdszVPRnLYlcEyMoyMQ4whkbAQyQYBAoH/aVVtfte+xFlJJAh4DuTBArw+HGhRHZ2CN1/uCrXkhmhNuEpN0k4AGxdFxSHAcynH/OTtTMBcckLmSaBwgg+LoNKQ4DT6bBl9oIMxFpJ8E8ieODkOPa5BKJPDgCASOy2bSgm2Io8OR4ZEiZMMQCgzETFpkpIBsiOP/rqBzCjwYIoEBzzebjU6E1Td9M+RDHL/doPMLPBpioQGnwW7S0JdrgIyIo9Ow/Dihcg08GtZCA2fFUNyIOLr8Pi5/wpY/EflZU651n4e0dA45Brj+KVv/VPS/1IqmcbQxxOXP2PJnIj9hPqP7ApAVUUPaEaUhZ9OQCw2E+8w814qoIQGJwlCwYSgEBsKGRLYMkCtRQ1YKhWH58b9sk5uGKPcQGCBHkuWdPcmehqQUSoPPpsEXGh4vDSlOQ8CmIRAacBqopBTsVtSQd0BhCNkwhAIDK1/dN9R8r/+kzcXDpxpQ/SO2/pHoT+hvk/qDLsbRcShwHGI2DrHgwFnqq3e6NVtfOFh+9IjsAlP/tejPMaz06u/o09/H9U/Y+ieiP+FJIUaUEDPj6DQEOA0pm4ZUaCCmQyJpgLyMo8MQ4jBkbBgygeFShxLkZRwdhgiHIWfDkAsMxNxYzTS0zTAvjk5DjNNQsGkohAbWMpB9vUbIvTg6DWuchjKTYLFzD5bQgMyVReWoYffi6DQkOA0+mwZfaMBpaOWo+9YIhdyLo9OQ4jQEbBoCoQGnoTXBal8mytI3vpDh+ods/UPRn7VIaF800Di+mOP6R2z9I9H/0snTNA4vFrj8MVv+WOS/1LAGuRc15BqmVK6BB8NaYCAMa2e7FzUkHlAYEjYMicBAWJToVWEh+6KGxANKQ8qmIRUacBrcvsl0YJOahmwDSkDGJiATAh4XARFOQM4mIBcCcAJoPztkU9SQYUBhKNgwFAIDZ2Ge3pXe7vVvdRS8EXIKqP5lhsBm5xRs0R/Rn17pD7Qpjo5DguPgs3HwBQcChxmJg60vHKS4/gFb/0D0J7wozXDQN8uao0//DNc/ZOsfiv6XLc2G2BRHpyHHaYjYNERCAzFdUpOGvmcYIJ/i6DQUOA0xm4ZYaGCt1NdnRoKMiqPTsPw4o5IMPBrWQgMxedaMNCNBRsXRafBxGhI2DYnQQEye5RL2A9ioODoNAU5DyqYhFRqIubQa/YY+DzPkUxwdhhCHIWPDkAkMOAwzAgbYpjg6DBEOQ86GIRcYcGuCyVjteXT5Y1z+gi1/IfITLjWq02jpHF5c4/qXuQOHnW1wRH98VU+8+mscXUxw+X22/L7Iz5lJra8rALkUNaQaUBgCNgyBwMAxpnFcihryDigMIRuGUGAgXElkwwCZFDWkHVAYIjYMkcCAw9BMQvfBALnVNGQdUBhiNgyxwPBoYVh+nFNJBx4Ma4EBg8Frp6AY1kUNOQcUhoQNQyIwENlpcpmve/lbMWI6QpIBlT9ly5+K/IT8RMOAGBdHpyHEacjYNGRCA2umFNS3OLr8ES5/zpY/F/kJ+clg4OiTP8blL9jyFyI/YUbxSDMK6FscHYc1jkOZNHDZaQZXcEAmSmri0Odih3yLo9OQ4DT4bBp8oYHwJs1IbxLkWxydhhSnIWDTEAgNl3qTINvi6DBkOAwhG4ZQYCBmzZpRMECuxdFhyHEYIjYMkcDAmUKL41ocHYYChyFmwxALDLhVwSJggF2Lo8Oguv+W+T9U5oHHw1p4wHlwyDSUpW+AwScJSNgEJEIAToBH+lU0jjAGJAEpm4BUCCDsa2QM0DjIGJIEZGwCMiGAs94jZ5pFDTkHioeczUMuPNCTaeE8QB5GDUkIioeCzUMhPFxqVoJsjBqyEBQPZVphwk5ETIQHxK9ET74Judc0JCIoIHw2EL4A8XiBSEkgAjYQgQCBA+GSLQbkaNSQjqB4CNk8hMIDkawkfUz3BLTImI2Qg6AIiNgEREIAayqNvjwEaGwcnYiCJCJmExELESwDQ980XLa+oFCmHywy/cBDYC0IEIt9uSQCjj4EfBKBhI1AIghcalwBLY6jAxGQQKRsIFIBgrPkWx8QkMlxdB5CkoeMzUMmPBATLbkUD5DNcXQeIpKHnM1DLjwQfibS3AY5HUfnISZ5KNg8FMIDYWki4wNkdhydhzXJQ5lq8NjJCU94QCxNzf4DZznp0YFISCB8NhC+AEHMztUAovsbE/Y8js5DSvIQsHkIhAech+baMMSa0qMjkJEIhGwEQkEAR4DqQ1o6Rx5zkoCITUAkBOCWFpsOAhpHHgsSgZiNQCwI4AhMzp62UUsywiaTETwe1sIDZwHJPh4g16OWzATOQ8LmIREeLp2VC3I9aklM4DykbB5S4eFSTxPkcdOSmMB5yNg8ZMLDo+UhInnI2TzkwgPOw+zsWRy1JCZwHgo2D4XwQCQuTXL2pnsE5jpyETgCZWZhys5FTAWBoYsE9c7YBJoeRyciIYnw2UT4QgRBBD2Hl60vKKQkAgEbgUAQIAwMzaCAL0Y9OgIZiUDIRiAUBIj1wsyzTY+jA5GTQERsICIBgjCxkEBApsfReShIHmI2D7HwQKwoR5pgIdPj6DyUuQmHzE3weFgLD4SpySNNTZDrcXQgfBKIhA1EIkBwTE0c1+PoPAQkDymbh1R4IExNZAcCMj2OzkNI8pCxeciEB8LhZBINBux6HB2IiAQiZwORCxCXrktp6Rt0iEkCCjYBhRCAE9DqQ6KmRy3pCJyAMrkwY6cjZkIATAA916fGgceEJMBnE+ALATgBc6KbCHseteQicB4CNg+B8IB7FmwqRw2bHrVkJnAgQjYQoQCBAzEhmwjI9KglMYHzELF5iIQHwtRETgULmdy0JCZwHmI2D7Hw8Gh5KBMTLpmY4PGwFh4wHqatRBXH9PiQPPySLbb5ZlEE7ZGm3y6SXf676t+KjLtuq3G6UfXvR5vViPQe4AkxgyFz4cjkgZhTYFpgHJwPJZqT0Rk5qGdBrCTsCJI8uQjygDS0hyXrmYMH4dByTlpjwJGqigygkLJRSAWF4eOTnMBgt8csRiAh+OhCJGRsEjIhYfg4JSsoOO3RilGCwgRCIWejkAsKwwcsOUHBbf8OGaPv8HEKkVCwSSiEBMZQJYOESfsXyAgkLOulLLsklGmpOTuRNRcSWGOUg0jw2l+M0jrczyXehcFnw+ALDOwBqUEwPORKE3ADcW+e7sIQsGEIBAb2aNQgGB7yEVy4jbgfoOzCELJhCAUGDAbv7A7D+A643hFDIrPFgyN6cnCM6pDsG7nu5+PScUjIDFP2/YlcFo+AWAg4Z+xxEAIPOfYIuWEIINZsINYCxBkjkIN4eMgRSMgMQ/CQsHlIhIdzxiEHAfGQ45CQG4YAImUDkQoQZ4xGDuLhIUcjITcMwUPG5iETHs4YkxzEw0OOSUJumFI74iEbHg+58HCpexLi4SFHJqGndAkeCjYPhfBwqVsO4mH0ZXADkgcVQRyTm7co9xAeznfLQTzomEKU4MFn8+ALD2cMUQ7i4bIhyqZoyW61LY56vO3qVUl0jPqleqhe9mRyvmKL7UqV2mq3VTcRJKUohrqNwN+/qi5YvUjU4VbbqIHPcrfL/Nz4chjl/VqPGZ/osb/VD6u/H07pnH66L7j7KxlaXu+eQHnZD1xezXjzIYjKz1sB520Va9514swCDzH54Wh18S5+1fjSZc4+lOFL+/qSGNSqyavbZLNaropjaW1KOf+4LYIsV/es5M+r6zq53XUQJL+oQ//bdp+RCnfZbbVNTSSziTgotugo9vZgsEZ1a0WZwy6/bt0ZL2IML87+xvbt0YnML1S107dWrC81lus7rFzf8VF9942hao9bpkC0bjrjT4qxGbuHFG8ngkMF/E3E8ccVxjGQv39CPZWXtoau3Q9PqMAeqryGBIvvqyDxQyc83PACw803EhJeuodCNA+FOHsyMeH9E0C8HbHHDAk/PqHyerAYOiQmvK9iwo+dmLDixYTVNxIT2iHhpflkYsIfngDj5YzJDX3GDAo/PYECsx+4vIbEhD9UMeGnTkz4Gy8m/O0biQl1YHWYMcH5RoKCKvBtrr7YH6t8HwW7KLjJFr//f1BLBwj1Wq9XwCsAAMS5AwBQSwECFAAUAAgACACvAYk/1je9uRkAAAAXAAAAFgAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc1BLAQIUABQACAAIAK8BiT/1Wq9XwCsAAMS5AwAMAAAAAAAAAAAAAAAAAF0AAABnZW9nZWJyYS54bWxQSwUGAAAAAAIAAgB+AAAAVywAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
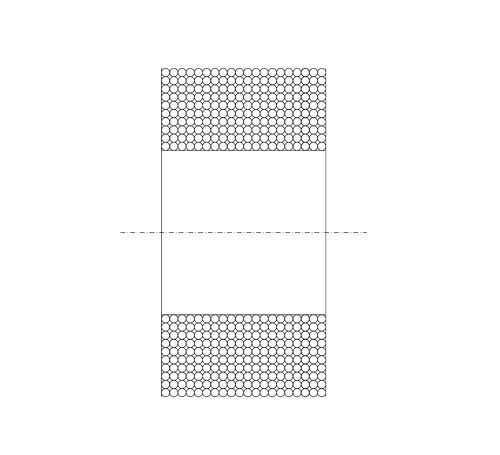
====Formel==== | ====Formel==== | ||
| + | <math>l= \frac{L}{r}\pi\sum_{x=1}^{n}</math> | ||
Version vom 9. Dezember 2011, 00:20 Uhr
Das Gast-Wiki im Geo-Wiki: Didaktik der anwendungsbezogenen Mathematik
Inhaltsverzeichnis |
Ideensammlung
Funktionales Denken
Proportionalität
- Größenbereiche
- Definition der Proportionalität
- Die Eigenschaften der Proportionalität nach Fricke
- Beispiele für Proportionale Zusammenhänge
Was ist, was soll Sachrechnen
Sachrechnen
Folien vom 18.11. als PDF (mit Office 2010 hat es dann doch geklappt.) Sachrechnen
Def. Sachrechnen (aus Greefrath. 2010. S. 12)
"Sachrechnen im weiteren Sinne bezeichnet die Auseinandersetzung mit der Umwelt, sowie die Beschäftigung mit wirklichkeitsbezogenen Aufgaben im Mathematikunterricht."
--Löwenzahn 16:24, 27. Nov. 2011 (CET)
Funktionen des Sachrechnens nach Winter
Sachrechnen als Lernstoff
Die mathematischen Inhalte des Sachrechnens stehen im Vordergrund. Greefrath setzt vorallem den Schwerpunkt auf die Inhalte der Größen, des Prozent- und Zinsrechnens. Allerdings ist der Inhalt stark davon abhängig wie der Mathematikunterricht gestaltet wird. Das Wichtige dabei ist, dass ein realitätsbezogener Kontext vorliegt. (Vgl. Greefrath. 2010. S. 13)
--Löwenzahn 16:31, 27. Nov. 2011 (CET)
Vermittlung von Größenvorstellungen
Längen
Flächeninhalte
Volumina
Zeit
Massen
Gewichte
Geschwindigkeiten
Dichten
Informationen
(Byte, GB, ....)
Sachrechnen als Lernprinzip
Sachrechnen als Lernziel
Komplexität von Sachrechenaufgaben
Simplex
Unter einem Simplex versteht man eine Struktur vom folgenden Typ:
Zwei Eingabedaten wird durch deren Verknüpfung mittels einer Rechenoperation ein Ausgabedatum zugeordnet.
Komplex
Unter einem Komplex versteht man die Verkettung mehrerer Simplexe. Man unterscheidet linerare und verzweigte Komplexe.
linearer Komplex
Verzweigter Komplex
Modellierung
Realsituation

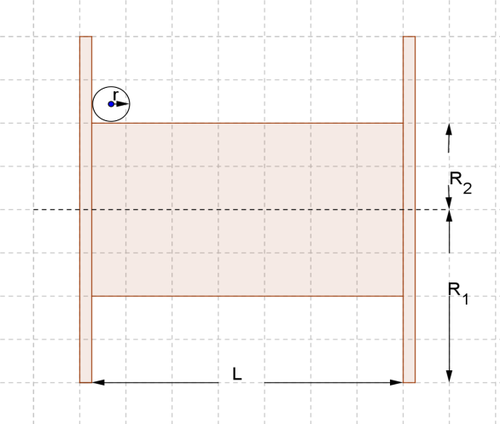
Wieviel m Kabel passt auf die Trommel?
Realmodell
mathematisches Modell
Kalkulationstabelle
Formel