Lösung von Aufg. 9.4 (WS 11/12): Unterschied zwischen den Versionen
Miriam (Diskussion | Beiträge) |
Miriam (Diskussion | Beiträge) |
||
| Zeile 47: | Zeile 47: | ||
* Die Argumentation für die einzelnen Fälle ist mir noch nicht ganz klar. Ich habe da etwas anders argumentiert, jedoch auch in diese drei Fälle unterschieden.Da es mir leider völlig rätselhaft ist, wie ich diese Tabelle hier erstellen soll, da mir dieses Programm überhaupt nicht liegt, versuche ich das einfach mal schriftlich zu erklären. | * Die Argumentation für die einzelnen Fälle ist mir noch nicht ganz klar. Ich habe da etwas anders argumentiert, jedoch auch in diese drei Fälle unterschieden.Da es mir leider völlig rätselhaft ist, wie ich diese Tabelle hier erstellen soll, da mir dieses Programm überhaupt nicht liegt, versuche ich das einfach mal schriftlich zu erklären. | ||
Ich habe die einzelnen Fälle zum Widerspruch geführt, indem ich bei den einzelnen Annahmen ( Beispielsweise: zw(A,B,C) ) anhand der Dreiecksungleichung geschlossen habe, dass dementsprechend AB + BC = AC gelten müsse. Zuvor haben wir gesagt, es existiert ein Punkt P mit P element AB und P element g (Definition Schnitt). Da P element AB ist muss es nun auch element AC sein (wegen der Dreiecksungleichung). | Ich habe die einzelnen Fälle zum Widerspruch geführt, indem ich bei den einzelnen Annahmen ( Beispielsweise: zw(A,B,C) ) anhand der Dreiecksungleichung geschlossen habe, dass dementsprechend AB + BC = AC gelten müsse. Zuvor haben wir gesagt, es existiert ein Punkt P mit P element AB und P element g (Definition Schnitt). Da P element AB ist muss es nun auch element AC sein (wegen der Dreiecksungleichung). | ||
| − | Ich hoffe, ich konnte diese Idee soweit nachvollziehbar rüberbringen :) Ganz ähnlich habe ich dann in den anderen Fällen argumentiert. Da nach dem speichern mal wieder Alles ganz falsch da stand, musste ich leider die Betragsstriche etc weglassen. An dieser Stelle sei erwähnt, dass sich sicherlich viel mehr Leute an den Lösungsdarstellungen beteiligen würden, wenn dies nicht so kompliziert wäre und so lange dauern würde. | + | Ich hoffe, ich konnte diese Idee soweit nachvollziehbar rüberbringen :) Ganz ähnlich habe ich dann in den anderen Fällen argumentiert. Da nach dem speichern mal wieder Alles ganz falsch da stand, musste ich leider die Betragsstriche etc weglassen. An dieser Stelle sei erwähnt, dass sich sicherlich viel mehr Leute an den Lösungsdarstellungen beteiligen würden, wenn dies nicht so kompliziert wäre und so lange dauern würde. --[[Benutzer:Miriam|Miriam]] 13:01, 10. Dez. 2011 (CET) |
Version vom 10. Dezember 2011, 13:01 Uhr
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
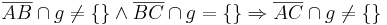
Vor.: 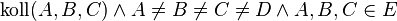
Beh.: 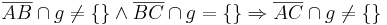
Beweis:
| Schritt | Begründung |
|---|---|
(1)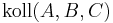 |
Vorr |
(2)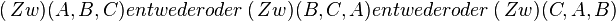 |
Dreiecksungleichung, Abstand kann nicht negativ sein |
(3)Fall 1: 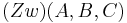 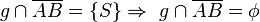 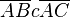 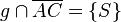 Behaupt stimmt Behaupt stimmt |
verschiedene Geraden haben höchstens einen Punkt gemeinsam, zw Relation, Teilmengenbezieung |
Fall 2: 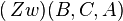 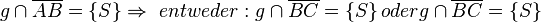 Wiederspruch zur Behauptung | |
Fall 3: 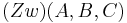 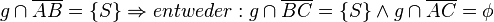 oder: g \cap \overline{AC}=\left\{ {S} \right\} \wedge g \cap \overline{BC}=\phi</math> oder: g \cap \overline{AC}=\left\{ {S} \right\} \wedge g \cap \overline{BC}=\phi</math>
| |
(4)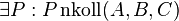 |
A I/3 |
(5) 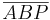 |
AI/1 |
(6) 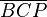 |
AI/1 |
(7) 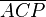 |
AI/1 |
(8) Fall 1: 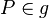 betrachte ich nachher betrachte ich nachher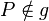 |
|
(9) 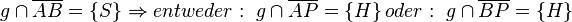 |
Axiom von Pasch ,(5) |
(10) 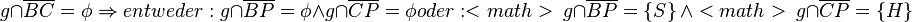 |
Axiom von Pasch ,(6) |
(11) 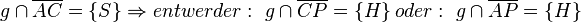 |
Axiom von Pasch ,(7) |
(12)  |
(3) |
(13) 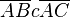 |
(12) |
(14) 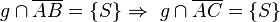 |
(9),10),(11),(13) |
Fall 2 von (7) analog nur mit 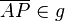
|
- Die Argumentation für die einzelnen Fälle ist mir noch nicht ganz klar. Ich habe da etwas anders argumentiert, jedoch auch in diese drei Fälle unterschieden.Da es mir leider völlig rätselhaft ist, wie ich diese Tabelle hier erstellen soll, da mir dieses Programm überhaupt nicht liegt, versuche ich das einfach mal schriftlich zu erklären.
Ich habe die einzelnen Fälle zum Widerspruch geführt, indem ich bei den einzelnen Annahmen ( Beispielsweise: zw(A,B,C) ) anhand der Dreiecksungleichung geschlossen habe, dass dementsprechend AB + BC = AC gelten müsse. Zuvor haben wir gesagt, es existiert ein Punkt P mit P element AB und P element g (Definition Schnitt). Da P element AB ist muss es nun auch element AC sein (wegen der Dreiecksungleichung). Ich hoffe, ich konnte diese Idee soweit nachvollziehbar rüberbringen :) Ganz ähnlich habe ich dann in den anderen Fällen argumentiert. Da nach dem speichern mal wieder Alles ganz falsch da stand, musste ich leider die Betragsstriche etc weglassen. An dieser Stelle sei erwähnt, dass sich sicherlich viel mehr Leute an den Lösungsdarstellungen beteiligen würden, wenn dies nicht so kompliziert wäre und so lange dauern würde. --Miriam 13:01, 10. Dez. 2011 (CET)

