Lösung von Aufg. 9.2 (WS 11/12): Unterschied zwischen den Versionen
RicRic (Diskussion | Beiträge) |
|||
| Zeile 13: | Zeile 13: | ||
<br /> | <br /> | ||
Ja Strecken sind schon endlich, aber meine Überlegung ist, dass bei der zweiten Strecke P eine Varialbe ist die irgendwo nach <math>\overline{AB}</math> sich befindet, also auch in der Unendlichkeit.--[[Benutzer:RicRic|RicRic]] 16:16, 11. Dez. 2011 (CET) | Ja Strecken sind schon endlich, aber meine Überlegung ist, dass bei der zweiten Strecke P eine Varialbe ist die irgendwo nach <math>\overline{AB}</math> sich befindet, also auch in der Unendlichkeit.--[[Benutzer:RicRic|RicRic]] 16:16, 11. Dez. 2011 (CET) | ||
| + | |||
| + | |||
| + | - Es seien zwie verschiedene Punkte A und B und g die Gerade durch A und B | ||
| + | AB+ ist die Steck AB und alle Punkte P für die gilt P ist Element von g und P ist nicht Element von AB. --[[Benutzer:Schmarn|Schmarn]] 10:49, 14. Dez. 2011 (CET) | ||
Version vom 14. Dezember 2011, 10:49 Uhr
Definieren Sie den Begriff Strahl 
. Verwenden Sie dabei den Begriff Strecke.
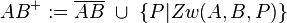--Todah raba 16:29, 7. Dez. 2011 (CET)
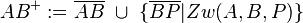--RicRic 21:50, 8. Dez. 2011 (CET)
- Eine dieser beiden Lösungsvorschläge stimmt nicht - aber welcher und warum nicht? --Spannagel 12:38, 10. Dez. 2011 (CET)
Bei der Definition von RicRic werden zwei Strecken vereinigt, die beide endlich sind. Das müsste falsch sein, da der Strahl AB^{+} in eine Richtung unendlich ist.
Wäre es auch möglich die Definition in einem Satz zu schreiben ? Mathenerds 12:27, 11. Dez. 2011 (CET)
Ja Strecken sind schon endlich, aber meine Überlegung ist, dass bei der zweiten Strecke P eine Varialbe ist die irgendwo nach 
sich befindet, also auch in der Unendlichkeit.--RicRic 16:16, 11. Dez. 2011 (CET)
- Es seien zwie verschiedene Punkte A und B und g die Gerade durch A und B
AB+ ist die Steck AB und alle Punkte P für die gilt P ist Element von g und P ist nicht Element von AB. --Schmarn 10:49, 14. Dez. 2011 (CET)
