Quiz der Woche: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 20: | Zeile 20: | ||
<quiz> | <quiz> | ||
<big>'''Die Idee, eine Klasse durch eines ihrer Elemente zu beschreiben.'''</big><br> | <big>'''Die Idee, eine Klasse durch eines ihrer Elemente zu beschreiben.'''</big><br> | ||
| − | {Wir wollen versuchen, die Art und Weise der Generierung einer beliebigen der Teilmengen <math>\ T_1, T_2, T_3, ..., T_n, ...</math> formal zu beschreiben. Diesbezüglich stellen wir fest, dass es sinnvoller ist, nicht mit Zahlen, sondern Elementen aus <math>\ M</math> zu indizieren. Unter der Klasse <math>\ T_a</math> verstehen wir dann alle Elemente von <math>\ M</math>, die mit dem Element <math>\ a</math> aus M in der Relation <math>\ R</math> stehen.} | + | {Wir wollen versuchen, die Art und Weise der Generierung einer beliebigen der Teilmengen <math>\ T_1, T_2, T_3, ..., T_n, ...</math> formal zu beschreiben. Diesbezüglich stellen wir fest, dass es sinnvoller ist, nicht mit Zahlen, sondern Elementen aus <math>\ M</math> zu indizieren. Unter der Klasse <math>\ T_a</math> verstehen wir dann alle Elemente von <math>\ M</math>, die mit dem Element <math>\ a</math> aus M in der Relation <math>\ R</math> stehen. Welche der folgenden formalen Definitionen ist bezüglich dieser Idee korrekt?} |
| − | + | + | + <math> \bigwedge_{a \in M}: T_a:= \lbrace b| b \in M \land bRa \rbrace </math> |
-Test | -Test | ||
</quiz> | </quiz> | ||
Version vom 16. Mai 2010, 16:28 Uhr
Es sei 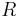 ein Äquivalenzrelation auf der Menge
ein Äquivalenzrelation auf der Menge  . Wir zerlegen
. Wir zerlegen  derart in Teilmengen
derart in Teilmengen 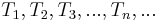 , dass gilt: Jede der Teilmengen besteht aus all den Elementen von
, dass gilt: Jede der Teilmengen besteht aus all den Elementen von  , die in der Relation
, die in der Relation 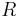 zueinander stehen.
zueinander stehen.
Übung zur Generierung einer Klasseneinteilung entsprechend obiger Idee.
Wir gehen von der folgenden Menge  aus:
aus:
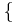 -26, 17, 75, -40, -13, 17, -55, -15, 7, -35, 95, 65, -9, 40, 3, 0,91, 70, -62, -22, 12, 26, 31,33, 50, -15, -100, -83, -61, -17
-26, 17, 75, -40, -13, 17, -55, -15, 7, -35, 95, 65, -9, 40, 3, 0,91, 70, -62, -22, 12, 26, 31,33, 50, -15, -100, -83, -61, -17 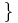
Die Relation 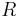 sei wie folgt festgelegt: Zwei Zahlen aus
sei wie folgt festgelegt: Zwei Zahlen aus  stehen in Relation zueinander, wenn sie bei Division durch 4 denselben Rest lassen. Da als Reste nur die Zahlen 0, 1, 2 und 3 in Frage kommen wird
stehen in Relation zueinander, wenn sie bei Division durch 4 denselben Rest lassen. Da als Reste nur die Zahlen 0, 1, 2 und 3 in Frage kommen wird  in 4 verschiedene Klassen entsprechend dieser Relation eingeteilt. Die Zahlen -40, 17, -26 und 75 gehören dementsprechend jeweils in eine eigene Klasse. Orden Sie die restlichen Zahlen durch Ziehen mit der Maus den richtigen Klassen zu.
in 4 verschiedene Klassen entsprechend dieser Relation eingeteilt. Die Zahlen -40, 17, -26 und 75 gehören dementsprechend jeweils in eine eigene Klasse. Orden Sie die restlichen Zahlen durch Ziehen mit der Maus den richtigen Klassen zu.
| -40 | 40 | 0 | 12 | -100 | |||||
| 17 | 17 | -55 | -15 | -35 | 65 | 33 | -15 | -83 | |
| -26 | 70 | -62 | -22 | 26 | 50 | ||||
| 75 | -13 | 7 | 95 | -9 | 3 | 91 | 31 | -61 | -17 |
Im folgenden soll bewiesen werden, dass die so gewonnenen Teilmengen von  eine Klasseneinteilung von
eine Klasseneinteilung von  sind. Ergänzen Sie dementsprechend die folgenden Ausführungen:
sind. Ergänzen Sie dementsprechend die folgenden Ausführungen:

