Quiz der Woche
Aus Geometrie-Wiki
Es sei 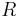 ein Äquivalenzrelation auf der Menge
ein Äquivalenzrelation auf der Menge  . Wir zerlegen
. Wir zerlegen  derart in Teilmengen
derart in Teilmengen 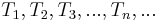 , dass gilt: Jede der Teilmengen besteht aus all den Elementen von
, dass gilt: Jede der Teilmengen besteht aus all den Elementen von  , die in der Relation
, die in der Relation 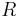 zueinander stehen.
zueinander stehen.
Satz:
Die Zerlegung von  in die Teilmengen
in die Teilmengen 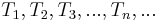 ist eine Klasseneinteilung von
ist eine Klasseneinteilung von  .
.
Beispiel zu dieser Idee, Klassen einzuteilen

