Lösung von Aufg. 12.6 WS 11/12: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „Beweisen Sie:<br /> <u>Korollar 1 zum schwachen Außenwinkelsatz</u><br /> ::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel. [[Category:Einfü…“) |
|||
| Zeile 3: | Zeile 3: | ||
::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel. | ::In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel. | ||
| + | Beweis: | ||
| + | Vor.: <math>\overline{ABC}</math> mit <math>\ \beta , \alpha & \gamma </math> | ||
| + | Beh.: <math>\ | \alpha | < 90 </math>, <math>\ | \beta | < 90 </math> | ||
| + | Ann.: <math>\ | \alpha | = 90 </math>, <math>\ | \beta | = 90 </math> | ||
| + | [[Datei:Bildschirmfoto 2012-01-15 um 13.31.23.png]] | ||
| + | |||
| + | 1) M sei Mittelpunkt von Strecke AB / Existenz und Eindeutigkeit des Mittelpunkts | ||
| + | 2) Es existiert C' Element MC- mit Abstand MC=MC' / Axiom vom Lineal | ||
| + | 3) lila Winkel = lila Winkel / Scheitelwinkelsatz | ||
| + | 4) Strecke AM kongruent zu MB / (1), Def. Mittelpunkt | ||
| + | 5) Strecke CM kongruent zu MC' / (2) | ||
| + | 6) Dreieck AMC kongruent zu Dreieck BMC / (3), (4), (5), SWS | ||
| + | 7) <math>\ | \alpha | =\angle C'BM = 90 </math> / (6), Vor. | ||
| + | 8) <math>\ | \beta | = | \delta | =90 </math> / Supplementaxiom, Vor. | ||
| + | 9) <math>\ | \delta | =\angle C'BM = 90 </math> / (7), (8) | ||
| + | 10) BC- kongruent zu BC'+ / (9),Winkelkonstruktionsaxiom | ||
| + | 11) C' ist Element von BC / (10) | ||
| + | 12) Analog lässt sich zeigen, dass C' Element von AB | ||
| + | 13) AC kongruent zu BC / (11), (12), Axiom I.1 | ||
| + | 14) koll(ABC) / 13), Def. koll -> Widerspruch zur Vorrausetzung | ||
| + | |||
| + | --[[Benutzer:Flobold|Flobold]] 13:56, 15. Jan. 2012 (CET) | ||
[[Category:Einführung_Geometrie]] | [[Category:Einführung_Geometrie]] | ||
Version vom 15. Januar 2012, 13:56 Uhr
Beweisen Sie:
Korollar 1 zum schwachen Außenwinkelsatz
- In jedem Dreieck sind mindestens zwei Innenwinkel spitze Winkel.
Beweis: Vor.:mit Fehler beim Parsen(Syntaxfehler): \ \beta , \alpha & \gamma
Beh.:,
Ann.:
,
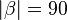
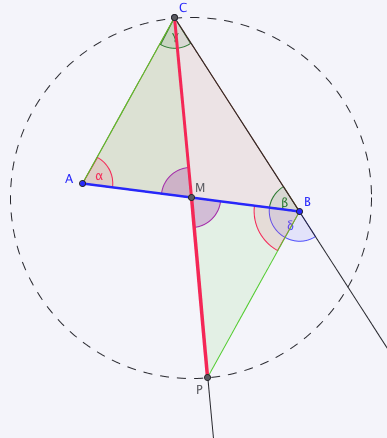
1) M sei Mittelpunkt von Strecke AB / Existenz und Eindeutigkeit des Mittelpunkts 2) Es existiert C' Element MC- mit Abstand MC=MC' / Axiom vom Lineal 3) lila Winkel = lila Winkel / Scheitelwinkelsatz 4) Strecke AM kongruent zu MB / (1), Def. Mittelpunkt 5) Strecke CM kongruent zu MC' / (2) 6) Dreieck AMC kongruent zu Dreieck BMC / (3), (4), (5), SWS 7)/ (6), Vor. 8)
/ Supplementaxiom, Vor. 9)
/ (7), (8) 10) BC- kongruent zu BC'+ / (9),Winkelkonstruktionsaxiom 11) C' ist Element von BC / (10)
12) Analog lässt sich zeigen, dass C' Element von AB
13) AC kongruent zu BC / (11), (12), Axiom I.1 14) koll(ABC) / 13), Def. koll -> Widerspruch zur Vorrausetzung
--Flobold 13:56, 15. Jan. 2012 (CET)