Zentrische Streckungen (2011/12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Definition II.07: (zentrische Streckung)) |
*m.g.* (Diskussion | Beiträge) (→Definition II.07: (zentrische Streckung)) |
||
| Zeile 2: | Zeile 2: | ||
==Begriff der zentrischen Streckung== | ==Begriff der zentrischen Streckung== | ||
===Definition II.07: (zentrische Streckung)=== | ===Definition II.07: (zentrische Streckung)=== | ||
| − | ::Es sei <math>Z</math> ein beliebig aber fest gewählter Punkt der Ebene <math>\varepsilon</math>. Ferner sei <math>k \in \mathbb{R} \setminus\left{ 0 \right}</math>. Unter der zentrischen Streckung <math>ZS_{Z,k}</math>mit dem Streckzentrum <math>Z</math> und dem Streckfaktor <math>k</math> versteht man eine Abbildung von <math>\varepsilon</math> auf sich mit <math>\forall P \in \varepsilon : ZS_{Z,k} (P) = Z + k \vec{ZP} </math>. | + | ::Es sei <math>Z</math> ein beliebig aber fest gewählter Punkt der Ebene <math>\varepsilon</math>. Ferner sei <math>k \in \mathbb{R} \setminus\left{ 0 \right}</math>. Unter der zentrischen Streckung <math>ZS_{Z,k}</math>mit dem Streckzentrum <math>Z</math> und dem Streckfaktor <math>k</math> versteht man eine Abbildung von <math>\varepsilon</math> auf sich mit <math>\forall P \in \varepsilon : ZS_{Z,k} (P) = Z + k \vec{ZP} </math>.<br /><br /> |
| + | Experimentieren Sie mit verschiedenen Werten von <math>k</math> und verschiedenen Positionen von <math>P</math> (Strg + f löscht die Spur):<br /><br /> | ||
<ggb_applet width="784" height="463" version="4.0" ggbBase64="UEsDBBQACAAIAE2KOEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAE2KOEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVhtb9s2EP7c/oqDUOzDmtii3ix3dou1QLEAaRcgXTEE+0JJtM1aEgWRsp2u++87kpIsJ2maN2xBE74d73jP3XOkOnuzK3LYsFpyUc4dMnIdYGUqMl4u506jFsex8+b189mSiSVLagoLURdUzZ1AS/IMO2HghTRZHNMspMfBNGDH8WIRHPvplCwYiYMw8hyAneSvSvGRFkxWNGXn6YoV9FSkVBnDK6WqV+PxdrsddaZGol6Ol8tktJOZA3jMUs6dtvMK1R1s2vpG3HNdMv7zw6lVf8xLqWiZMge0Cw1//fzZbMvLTGxhyzO1mjuxi26sGF+u0KdID8ZaqEJAKpYqvmEStw6GxmdVVI4Ro6Vef2Z7kPfuOJDxDc9YPXfckRc6IGrOStWuktbKuNs/23C2tYp0z+LqgBIiT6jWAd++ged6LhzphtjGwyaK7JJr51zfNp5tAtuEViaw2wMrGliZwMoEvgMbLnmSs7mzoLlEzHi5qDFe/Viqy5yZ87QTe3/JEfok+VcU9jWIFmScd90j/YvIHgUdugMnycCqqpt7Gu1MTuLg7ia9Rznqdza9m9z0wu+4Gd1i1Pp9Fz9JOLCJpsw/83vNon+bm1ct2vHjDEbBf+LibNxRZdayA+RKy7bZo1ghNV/8KYRTnfYEQuRGNMEsD4FMsZl4gGwAEkIQ4pDEEOl2Av4EFwLwIQYtR3ww5Ahj/BNMjLIIQlSmZyfISSBoKIDQB2I4FQAyCQwvkaOejxJhCCFu0uaJp1X4EQQRjvwYAjyjpuSEoKCPG3GM5j3wCfh6M5mAF0Gk9ZFAUz2K9dFRpQeRCxHRCpHVyGjLZpSPwdfeRC1cvKwadQBRWmRdV4mqjwVKYz3a1zlbnw7K4LNZThOW481wriMJsKG5ZoQxtBClgi6Inp1b1rRa8VSeM6Vwl4QvdENPqWK79ygtO9tGNhWlPKuFeifypiglQCpytz+zyMmg7/WnxoE/WAiGC+FgIRr0JzfaFbgCjWRoX9SyE6dZdqIl9qUBkfy9zC/f1oyuK8EP3ZiNzSUzY02a84zT8jMmq7aicYHuzjHlqrtzAj/sDiLq7PxSYgbD7oLVAqH1J/qWvbQjL8LbefiDMZYp1XwLpqPpwQ9uapdC93ATsdbYpg8K3bG9f8ua9+mh+yfyrcizftl4/I5WqqnNAwHLYa39+LVc5sxkhSmwePum60Tszm06+FbXp8sKR649QLI0SANWAy/EC3LZtoltjYw+WS/lGhnXSLhdfvGsXydTz0iYNrGtkcKEtUdrPSWdl8TtzHBpapjrtEzp6pNOd32ZNyVXp91A8XTdukrsho9NkbA+aQ51kqfSORtfyarZmtUly9skxlg2opGWk4P8zljKCxzahRYSqsP1Bx7AzmZsWbPu4Ll5fFnAzKo7zM9r00bV+1oUJ+XmE+bClQPMxt0pZzKteaVTDhIs/Gu2z6qMS4r3Rjbcp1mHrqf6fkB4lIYG+diolajN+wrLCLaabDkr8G0FyqSXydAe5gvzTNN4gki+YCXrLzu7vg8YLt+YaiYpaV6tqH7KtU7n9JLVBzAYfR9Exg6KIi0Re+MB0rrSCnR0K8ZsYtgTY6dChYZPB4UJ8Zaws2bhsm2/2ke6faVqXzXHDoza2evxQ9bqk5i5Fxcv2pyy4F2DsWwKVvO0B2ptgMS9TauVjKZW72PAdQfQkjtC28rJXD+voeD4ejjGEBUUkdKhSiTeIAo/MDCly/0Hhj1ZW4Hxraax3OnXagtuaDoLvhvkJaYa/4rUogfO7OuJwsttjS94aYqeasub6fzGs4yV/WnvlAjuTYnw/RAdZvrZ/5vpqsaPOjszKIJPkv7eaBqYEJFR6D0ZAc6uESAVRUHLDErzZP2MEIra2b+hqKvLCVCisbZANqpbaKyyVsW1UG2ssi4WzaNj5T48UrcBu1d2U45P+5CFNyb54IaQ9i5Laa2YxBur5azC8ZmODrBdpeG8ITB/IVh/X5z9c71A7aoaz6Elu5z/iVZC/uK02uAlrOFnaJxDgox/xJxWy0Nior96lrZJbPOkBNrHKhyFcXjlhacjGMfx01HCAjG/eLn+bhDuQZIW1qtU2dyLKpsfhGVQMYZx6Z6UD2eLe98I3M6d8Pb74WHUGQZmPHwwmS+R9r/RXv8LUEsHCBNS0TdOBgAA4xMAAFBLAQIUABQACAAIAE2KOEDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgATYo4QBNS0TdOBgAA4xMAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADlBgAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | <ggb_applet width="784" height="463" version="4.0" ggbBase64="UEsDBBQACAAIAE2KOEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIAE2KOEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1sxVhtb9s2EP7c/oqDUOzDmtii3ix3dou1QLEAaRcgXTEE+0JJtM1aEgWRsp2u++87kpIsJ2maN2xBE74d73jP3XOkOnuzK3LYsFpyUc4dMnIdYGUqMl4u506jFsex8+b189mSiSVLagoLURdUzZ1AS/IMO2HghTRZHNMspMfBNGDH8WIRHPvplCwYiYMw8hyAneSvSvGRFkxWNGXn6YoV9FSkVBnDK6WqV+PxdrsddaZGol6Ol8tktJOZA3jMUs6dtvMK1R1s2vpG3HNdMv7zw6lVf8xLqWiZMge0Cw1//fzZbMvLTGxhyzO1mjuxi26sGF+u0KdID8ZaqEJAKpYqvmEStw6GxmdVVI4Ro6Vef2Z7kPfuOJDxDc9YPXfckRc6IGrOStWuktbKuNs/23C2tYp0z+LqgBIiT6jWAd++ged6LhzphtjGwyaK7JJr51zfNp5tAtuEViaw2wMrGliZwMoEvgMbLnmSs7mzoLlEzHi5qDFe/Viqy5yZ87QTe3/JEfok+VcU9jWIFmScd90j/YvIHgUdugMnycCqqpt7Gu1MTuLg7ia9Rznqdza9m9z0wu+4Gd1i1Pp9Fz9JOLCJpsw/83vNon+bm1ct2vHjDEbBf+LibNxRZdayA+RKy7bZo1ghNV/8KYRTnfYEQuRGNMEsD4FMsZl4gGwAEkIQ4pDEEOl2Av4EFwLwIQYtR3ww5Ahj/BNMjLIIQlSmZyfISSBoKIDQB2I4FQAyCQwvkaOejxJhCCFu0uaJp1X4EQQRjvwYAjyjpuSEoKCPG3GM5j3wCfh6M5mAF0Gk9ZFAUz2K9dFRpQeRCxHRCpHVyGjLZpSPwdfeRC1cvKwadQBRWmRdV4mqjwVKYz3a1zlbnw7K4LNZThOW481wriMJsKG5ZoQxtBClgi6Inp1b1rRa8VSeM6Vwl4QvdENPqWK79ygtO9tGNhWlPKuFeifypiglQCpytz+zyMmg7/WnxoE/WAiGC+FgIRr0JzfaFbgCjWRoX9SyE6dZdqIl9qUBkfy9zC/f1oyuK8EP3ZiNzSUzY02a84zT8jMmq7aicYHuzjHlqrtzAj/sDiLq7PxSYgbD7oLVAqH1J/qWvbQjL8LbefiDMZYp1XwLpqPpwQ9uapdC93ATsdbYpg8K3bG9f8ua9+mh+yfyrcizftl4/I5WqqnNAwHLYa39+LVc5sxkhSmwePum60Tszm06+FbXp8sKR649QLI0SANWAy/EC3LZtoltjYw+WS/lGhnXSLhdfvGsXydTz0iYNrGtkcKEtUdrPSWdl8TtzHBpapjrtEzp6pNOd32ZNyVXp91A8XTdukrsho9NkbA+aQ51kqfSORtfyarZmtUly9skxlg2opGWk4P8zljKCxzahRYSqsP1Bx7AzmZsWbPu4Ll5fFnAzKo7zM9r00bV+1oUJ+XmE+bClQPMxt0pZzKteaVTDhIs/Gu2z6qMS4r3Rjbcp1mHrqf6fkB4lIYG+diolajN+wrLCLaabDkr8G0FyqSXydAe5gvzTNN4gki+YCXrLzu7vg8YLt+YaiYpaV6tqH7KtU7n9JLVBzAYfR9Exg6KIi0Re+MB0rrSCnR0K8ZsYtgTY6dChYZPB4UJ8Zaws2bhsm2/2ke6faVqXzXHDoza2evxQ9bqk5i5Fxcv2pyy4F2DsWwKVvO0B2ptgMS9TauVjKZW72PAdQfQkjtC28rJXD+voeD4ejjGEBUUkdKhSiTeIAo/MDCly/0Hhj1ZW4Hxraax3OnXagtuaDoLvhvkJaYa/4rUogfO7OuJwsttjS94aYqeasub6fzGs4yV/WnvlAjuTYnw/RAdZvrZ/5vpqsaPOjszKIJPkv7eaBqYEJFR6D0ZAc6uESAVRUHLDErzZP2MEIra2b+hqKvLCVCisbZANqpbaKyyVsW1UG2ssi4WzaNj5T48UrcBu1d2U45P+5CFNyb54IaQ9i5Laa2YxBur5azC8ZmODrBdpeG8ITB/IVh/X5z9c71A7aoaz6Elu5z/iVZC/uK02uAlrOFnaJxDgox/xJxWy0Nior96lrZJbPOkBNrHKhyFcXjlhacjGMfx01HCAjG/eLn+bhDuQZIW1qtU2dyLKpsfhGVQMYZx6Z6UD2eLe98I3M6d8Pb74WHUGQZmPHwwmS+R9r/RXv8LUEsHCBNS0TdOBgAA4xMAAFBLAQIUABQACAAIAE2KOEDWN725GQAAABcAAAAWAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYV9qYXZhc2NyaXB0LmpzUEsBAhQAFAAIAAgATYo4QBNS0TdOBgAA4xMAAAwAAAAAAAAAAAAAAAAAXQAAAGdlb2dlYnJhLnhtbFBLBQYAAAAAAgACAH4AAADlBgAAAAA=" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "true" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /> | ||
Version vom 24. Januar 2012, 17:20 Uhr
Zentrische Streckungen
Begriff der zentrischen Streckung
Definition II.07: (zentrische Streckung)
- Es sei
 ein beliebig aber fest gewählter Punkt der Ebene
ein beliebig aber fest gewählter Punkt der Ebene  . Ferner sei Fehler beim Parsen(Syntaxfehler): k \in \mathbb{R} \setminus\left{ 0 \right}
. Ferner sei Fehler beim Parsen(Syntaxfehler): k \in \mathbb{R} \setminus\left{ 0 \right}
- Es sei
. Unter der zentrischen Streckung 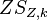 mit dem Streckzentrum
mit dem Streckzentrum  und dem Streckfaktor
und dem Streckfaktor  versteht man eine Abbildung von
versteht man eine Abbildung von  auf sich mit
auf sich mit 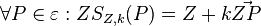 .
.
Experimentieren Sie mit verschiedenen Werten von  und verschiedenen Positionen von
und verschiedenen Positionen von  (Strg + f löscht die Spur):
(Strg + f löscht die Spur):

