Zusatzaufgaben 2 S (SoSe 12): Unterschied zwischen den Versionen
Aus Geometrie-Wiki
(Die Seite wurde neu angelegt: „== Aufgabe 1 == Wir gehen von folgender Implikation aus: Wenn zwei Winkel Nebenwinkel sind, so sind sie supplementär.<br /> a) Wie lautet die Kontraposition dies…“) |
|||
| (Eine dazwischenliegende Version von einem Benutzer wird nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
== Aufgabe 1 == | == Aufgabe 1 == | ||
| − | + | Definieren Sie den Begriff ''Mittelpunkt einer Strecke'' (Strecke sei bereits definiert). | |
| − | + | ||
| − | + | ||
| − | [[Lösung von Zusatzaufgabe 2. | + | [[Lösung von Zusatzaufgabe 2.1_neu (SoSe_12)]] |
| − | == Aufgabe 2 == | + | == Aufgabe 2 == |
| + | Definieren Sie den Begriff ''Quadrat'' auf mindestens drei verschiedene Weisen.<br /> | ||
| + | |||
| + | [[Lösung von Zusatzaufgabe 2.2_neu (SoSe_12)]] | ||
| + | |||
| + | |||
| + | == Aufgabe 3 == | ||
| + | Definieren Sie den Begriff ''Dreieck''.<br /> | ||
| + | |||
| + | [[Lösung von Zusatzaufgabe 2.3_neu (SoSe_12)]] | ||
| + | |||
| + | |||
| + | == Aufgabe 4 == | ||
| + | Definieren Sie den Begriff ''Kugel''.<br /> | ||
| + | |||
| + | [[Lösung von Zusatzaufgabe 2.4_neu (SoSe_12)]] | ||
| + | |||
| + | |||
| + | == Aufgabe 5 == | ||
Beweisen Sie mit Hilfe einer Wahrheitstabelle:<br /><br /> | Beweisen Sie mit Hilfe einer Wahrheitstabelle:<br /><br /> | ||
<math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> | <math>(\ A \Rightarrow B) \ \Leftrightarrow (\neg B \Rightarrow \neg A)</math><br /> | ||
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br /> | Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?<br /> | ||
| − | [[Lösung von Zusatzaufgabe 2. | + | [[Lösung von Zusatzaufgabe 2.5_neu (SoSe_12)]] |
| + | |||
| − | |||
| − | |||
| − | |||
| − | [[ | + | [[Category:Einführung_S]] |
Aktuelle Version vom 26. April 2012, 12:46 Uhr
Inhaltsverzeichnis |
Aufgabe 1
Definieren Sie den Begriff Mittelpunkt einer Strecke (Strecke sei bereits definiert).
Lösung von Zusatzaufgabe 2.1_neu (SoSe_12)
Aufgabe 2
Definieren Sie den Begriff Quadrat auf mindestens drei verschiedene Weisen.
Lösung von Zusatzaufgabe 2.2_neu (SoSe_12)
Aufgabe 3
Definieren Sie den Begriff Dreieck.
Lösung von Zusatzaufgabe 2.3_neu (SoSe_12)
Aufgabe 4
Definieren Sie den Begriff Kugel.
Lösung von Zusatzaufgabe 2.4_neu (SoSe_12)
Aufgabe 5
Beweisen Sie mit Hilfe einer Wahrheitstabelle:
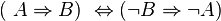
Inwiefern hilft Ihnen diese Äquvalenz, wenn Sie einen geometrischen Satz beweisen wollen?
Lösung von Zusatzaufgabe 2.5_neu (SoSe_12)

