Lösung von Aufgabe 1.6 (SoSe 12): Unterschied zwischen den Versionen

Aus Geometrie-Wiki
Wechseln zu: Navigation, Suche
(→‎Kommentar M.G)
 
(16 dazwischenliegende Versionen von 7 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
 
In welchen Fällen handelt es sich um eine korrekte Definition des Begriffs Parallelogramm? Begründen Sie!<br />
 
In welchen Fällen handelt es sich um eine korrekte Definition des Begriffs Parallelogramm? Begründen Sie!<br />
−
# Wenn sich in einem Viereck die Diagonalen halbieren, so ist das Viereck ein Parallelogramm.
+
1) Wenn sich in einem Viereck die Diagonalen halbieren, so ist das Viereck ein Parallelogramm.<br />
−
# Wenn in einem Drachen die gegenüberliegenden Seiten kongruent zueinander sind, so ist der Drachen ein Parallelogramm.
+
2) Wenn in einem Drachen die gegenüberliegenden Seiten kongruent zueinander sind, so ist der Drachen ein Parallelogramm.<br />
−
# Es gibt Trapeze, die ein weiteres Paar paralleler Seiten haben und die Parallelogramme genannt werden.
+
3) Es gibt Trapeze, die ein weiteres Paar paralleler Seiten haben und die Parallelogramme genannt werden.<br />
−
# Trapeze mit zwei zueinander kongruenten Seiten heißen Parallelogramme.<br />
+
4) Trapeze mit zwei zueinander kongruenten Seiten heißen Parallelogramme.<br />
 +
 
 +
 
  
  
Zeile 10: Zeile 12:
 
[[Kategorie:Einführung_P]]
 
[[Kategorie:Einführung_P]]
 
[[Kategorie:Einführung_S]]
 
[[Kategorie:Einführung_S]]
 +
 +
 +
1) nicht ausreichend, da bei einem Rechteck genau das Gleiche gilt<br />
 +
2) in Ordnung --> es sind die Eigenschaften gegeben, dass die zwei Paare der Seiten parallel zueinander sind und gleich lang<br />
 +
3) in Ordnung<br />
 +
4) nicht ausreichend, da es eher heißen müsste: Trapeze mit zwei Paar zueinander kongruenten Seiten heißen Parallelogramme. <br />
 +
-- [[Benutzer:Nala23|Nala23 ]]    14:04, 22. Apr. 2012<br />
 +
Was meinen denn die anderen dazu? Hier bietet es sich meiner Meinung nach an, auf die Lösungsvorschläge von Nala23 einzugehen und nicht nur eine weitere Lösung einzustellen.--[[Benutzer:Andreas|Tutor Andreas]] 18:47, 22. Apr. 2012 (CEST)
 +
 +
 +
Ich hätte zu 2) gasagt, dass man man diese beiden geometrischen Figuren (Drachen und Parallelogramm) nicht aufeinander beziehen kann (siehe Haus der Vierecke). <br />
 +
 +
 +
Derjenige möchte Parallelogramm definieren, dann sollte man als Oberbegriff Trapez oder Viereck/n-Eck mit n=4 benutzen.<br />
 +
Bei Nala23s Kommentaren zu 1) und 3) stimme ich zu.<br />
 +
Zu 4) hätte ich gesagt: Trapeze, bei deen die gegenüberliegenden Seiten stets parallel sind heißten Parallelogramme. --[[Benutzer:Honeydukes|Honeydukes]] 23:06, 22. Apr. 2012 (CEST)<br />
 +
Mh? zu 1) für Rechtecke gilt das auch, das stimmt. Na und? <br />
 +
zu 2)und 3) überlegt nochmal...--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:32, 24. Apr. 2012 (CEST)
 +
 +
<br />
 +
<br />
 +
''Zu 4:<br />
 +
''Alle Parallelogramme gehören zur Klasse der Trapeze, schiefer Drachen und Vierecke. Sie sind ein Oberbegriff für Parallelogramme und können damit auch definiert werden. (vgl. Haus der Vierecke, in Didaktik der Geometrie für die Sekundarstufe 1,S.137) oder vgl. http://wikis.zum.de/geowiki/Haus_der_Vierecke_%2815.07.2011%29<br /> <br /> Habe gerade festgestellt, dass sich meine beiden Quellen widersprechen. Sind meine Definitionen nun falsch? Oder hab ich einen Denkfehler?<br />
 +
 +
 +
''1. Ein Trapez/schiefer Drachen/Viereck mit zwei Paaren paralleler Gegenseiten ist ein Parallelogramm.<br />
 +
''2. Ein Trapez/schiefer Drachen/Viereck mit sich gegenseitig halbierenden Diagonalen ist ein Parallelogramm.<br />
 +
''3. Ein Trapez/schiefer Drachen/Viereck mit einem Paar paralleler und zueinander kongruenter Seiten ist ein Parallelogramm.<br /><br />
 +
''Bei Betrachtung meiner dritten Definiton fällt auf, dass sie fast der ursrünglichen entspricht - zwei konkruente Seiten sind in der Definiton gegeben, es fehlt meiner Meinung nach der Verweis auf ein paar paralleler konkruenter Seiten.--[[Benutzer:Braindead|Braindead]] 15:26, 23. Apr. 2012 (CEST)
 +
<br />
 +
Ja richtig, das ist eine Möglichkeit: Deine dritte Definition verbessert Nr. 4 der Aufgabenstellung. Wenn du schreibst "Ein Viereck mit..." und dann "ein Trapez mit", dann brauchst du bei zweiterem meist weniger zusätzliche Eigenschaften nennen, da ja das Trapez schon Eigenschaften in die Definition miteinbringt. Deshalb kann man so "Trapez/schiefer Drachen/Viereck" schlecht beurteilen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 14:32, 24. Apr. 2012 (CEST)
 +
 +
3) ist eine Aussage und keine Definition. Es handelt sich hier also um das selbe Problem wie in Aufgabe 1.5.--[[Benutzer:KeinKurpfälzer|KeinKurpfälzer]] 20:11, 24. Apr. 2012 (CEST)
 +
 +
==Kommentar M.G==
 +
 +
:: In 3. wird behauptet, dass irgendetwas existiert. Es obliegt uns nicht mittels einer Definition festzulegen, dass etwas existiert oder nicht (wir und auch die Mathematiker  sind nicht Gott oder ein anderes höheres Wesen). Wir müssen die objektive Realität so nehmen wie sie ist. Wir können den Dingen nur Namen geben und fertig. User KeinKurpfälzer hat also Recht.--[[Benutzer:*m.g.*|*m.g.*]] 22:17, 24. Apr. 2012 (CEST)
 +
 +
::Es ist nicht egal für die Definition eines Begriffs, auf welchen Oberbegriff man sich bezieht:
 +
::: 1. Beziehe ich mich für die Definition des Begriffs ''Parallelogramm'' auf den Oberbegriff ''Viereck'', dann muss ich festlegen, dass unser Viereck zwei Paare paralleler Seiten hat: Wenn ein ''Viereck'' zwei Paare  paralleler Seiten hat, so heißt es ''Parallelogramm''.
 +
::: 2. Beziehe ich mich auf den Oberbegriff ''Trapez'', so brauche ich nur ein weiteres Paar paralleler Seiten zu fordern, denn jedes ''Trapez'' hat ja bereits ein solches: Wenn ein ''Trapez'' ein weiteres Paar zueinander paralleler Seiten besitzt, so heißt es ''Parallelogramm''.
 +
::: 3. Will ich den relativ selten verwendeten Oberbegriff ''schiefer Drachen'' verwenden, so macht es Sinn, zunächst die Definition für den Begriff ''schiefer Drachen'' zu betrachten: Wenn eine Diagonale eines Vierecks die andere Diagonale dieses Vierecks halbiert, so ist das Viereck eine schiefer Drachen. In jedem Parallelogramm halbieren sich die Diagonalen gegenseitig. Also gibt es in jedem Parallelogramm eine Diagonale , die die  halbiert: Jedes Parallelogramm ist somit ein schiefer Drachen. Das Besondere eines jeden schiefen Drachens, der auch als Parallelogramm bezeichnet werden darf ist, dass in einem solchen schiefen Drachen nicht nur die eine Diagonale die andere sondern auch die andere die eine Diagonale halbiert (meint sie halbieren einender gegenseitig): Es sei <math>\overline{ABCD}</math> ein schiefer Drachen, wobei die Diagonale <math>\overline{AC}</math> die Diagonale <math>\overline{BD}</math> halbieren möge. Wenn auch die Diagonale <math>\overline{BD}</math> die Diagonale  <math>\overline{AC}</math> halbiert, so heißt der <math>schiefe Drachen</math> <math>\overline{ABCD}</math> ''Parallelogramm''.--[[Benutzer:*m.g.*|*m.g.*]] 22:17, 24. Apr. 2012 (CEST)
 +
 +
<br />
 +
''Frage zur Definition schiefer Drachen in 3.: Wo halbieren sich die Diagonalen in einem schiefen Drachen?--[[Benutzer:Braindead|Braindead]] 09:51, 25. Apr. 2012 (CEST)<br /><br />
 +
<ggb_applet width="496" height="319"  version="4.0" ggbBase64="UEsDBBQACAAIADtYnEAAAAAAAAAAAAAAAAAWAAAAZ2VvZ2VicmFfamF2YXNjcmlwdC5qc0srzUsuyczPU0hPT/LP88zLLNHQVKiuBQBQSwcI1je9uRkAAAAXAAAAUEsDBBQACAAIADtYnEAAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1s3Vptb9s4Ev7c/RWEPhzucInNF4mSe3YXaYrFFYi3xSV3WNzuYkFJtM2NLGkl2rF7e//9hqRkS3Hemra3SYPafBvOcGaemaHkjr/dLDO0llWtinzikQH2kMyTIlX5fOKt9Ow48r599c14Lou5jCuBZkW1FHri+YZSpRMv4YQlJGLHPpbwRejoWJA0OA5DnKazWSyFjD2ENrV6mRffi6WsS5HI82Qhl+KsSIS2ghdaly+Hw6urq0EralBU8+F8Hg82deohOGZeT7ym8xLY9TZdMUtOMSbDH6Znjv2xymst8kR6yKiwUq++eTG+UnlaXKErlerFxAsI9dBCqvnC6BRwDw0NUQkGKWWi1VrWsLUztDrrZelZMpGb9Reuh7KdOh5K1Vqlspp4eMBGmNPAQ0WlZK4bCtJIGrY8xmslrxwz07NyfA/poshiYfig339HFFOMjkxDXEOh4dwtYTeHmWuoa3zXBI7Gd9t9R+o7Gt/R+MxDa1WrOJMTbyayGuym8lkFPtuNa73NpD1PM7HXmRyBTrX6AMQMAzicoWEe4yPz4fDxzcKwryTpSNXV6iOFtiL9EX+4SPpJirJWJr1JTRrcoia/Q6jT+yF6kqAjE0TZf/ZzIJHdpeZ1iW78aQK5/39RcTxsQ2XcRAeqF4a2QY+Wy9rECxuhYGRgT1AAscFDQHmAyAiakCKIBkQC5AcwJBHipg0RC2HBRwxFyNARhmxwBBF8+aFlxlEAzMxsCDGJCAjyUcAQsTHlI4gkZOMSYpQyoAgCFMAmI55Qw4Jx5HMYsQj5cEYTkiEBQgYbYQziKWIEMbOZhIhyxA0/4ptQ55E5OrCkiGPEiWEIUQ0R7aIZ6CPEjDZtMlN5udI9EyXLtO3qotz5AqghH+1znctPvVT4YpyJWGZQHc6NJxFai8xEhBU0K3KNWidSNzevRLlQSX0utYZdNfpVrMWZ0HLzHVDXrWxLmxR5/b4q9GmRrZZ5jVBSZHh35iIjnT7dnRoGrLPgdxeCzgLv9MMb5Rawgla1BPlFVbfkIk3fGop9agBLvsuz7etKisuyUH01xkNbaMZylWQqVSL/F4DVSDF2QW3dsemqrTt0RNqDFFV6vq0BwWjzb1kVsEYCU2m3bsTMqPsHXOpEmHgLsKXrjLp/jYfkeucHsZF7leaVid/O4G39usj2U1bLU1HqVWUvBpACK3P2k3yeSYsEm1Sh6iaXcbE5dxBgjtfFtoQRdieI59a6CDIADaAozps2dq2lMUfbUWFLgy0FbjGl0t06GVFLYdvYtZYKQOqO1qhKWjUJbsWo2uYt7DXR0eYkA3FTxFe50mftQKvkslGVuA3fr5ax3AGlz5N8Lp7j4TUkjS9llcusAS44c1WsaheHHUynMlFLGLqFxiTCuOufcAA3m8p5JduDZ/bS5QxmV3EXkwfTltV3VbF8m68vAAvXDjAetqcc10mlSoM5FEOyv5R7VKWqFlAr0u4+E2mgemJqAphHG9NADK70oqjsvQpSB7QmwDK5hPsU0hZeFqE7M5/Y65mxJyriXyF77QqcW987DJZvhJoFpcjKhTBXuEbpTGxl1TOD5Tct0uvGAdtbDSCUS+fbUkoHC3de6JTAzkZTLxWBtWu0mXjH9i6+hZOY9oO7m7vLqVHVhFgv+brZa34C8Dgr3WOv06/CXpG1lz/g9LMYLCmWS5GnKLf3l3M5N/PevqIKbICGBDH2c8ZZ6XZBOG4NjwPz1w231sDiHgd0VL7NA/jx9u9YkVrrgRmPsbHnBwfEg5SqoaZfwoNLbfO+bjK87fxdpam09zlXcn7L3Zba5Tm1LDOVKL2zWGac+jbXkPWkDfvDZHYpZWmqyLv8ohJ5bZ5BHU0nSd7itqlKHdT7fhMHDpve7bB+vEwfFS/mfjx3Teyaz+AwMvCtv9iAkS+eJ15/BXmCDShvLRZ9gUTxD7G9BrbXLklMDzAX3425Cji1lo2fSIKArXzU/Ysc/CD7Br35kUsefICDiD/b9PH+htwRH/jxzcfkjjePiiFC3WXZtk8hjvxBFLFRSPDI5yGnNGxiCocswNznPgmjKKDsC0TY+yLbzov85lJsgo2aiowEazzT8xVcojN4SiGOWvxCHH1sO7AjgQaeIdP7XOqO0Dptx/WxOP/oyCYBs4AIyEFwk49Bw+2p/+CO8gt5XBK646ifUveYu+/BlcUk9A8GfIT1UlD4jPLO3baPn5jtqd97vUCbGuAH1+xva0A0GIXhc7pC3u2L5Ol4ggwCyLQjFrAgooT4oQsJPuC93MwD5wgaDfCI0yDCIzqinLSvhb4Cp6RPySmHNdDkqeCwYprSSAeRT3w/4uBERhgOnpFP+nX5jWp+busX5umtz8ixoU+np3fX2ny1lJVK9nVot83wg7OtGk9ASeCjEIdwKcVh5APuH34hJgdw25QV2Nxckhq5F3KjQSiClYn3p99Whf7bT8VaVsZT/3Fj9Ff0Z/Mb54/Tn/+y65/aviP4L/rpCE3M127DXh37Ar6vuwaZ3rUD/JEPAqo+Exfyhz4imjf/NXhptn9Lbt8BY6/FYsMAdK20vVU7O7bP5z9Oj9Dpzx3R72azWmobT0380Eeh7+S2h6/G7if3PPjfgr6T6R+APhD6IPSddNA3fRD6DOcHoO/kvhcfzxV9J0doegv63FvYY3Lgo2H3XbX94af5nwuv/gdQSwcIXbaWjdwHAABWIQAAUEsBAhQAFAAIAAgAO1icQNY3vbkZAAAAFwAAABYAAAAAAAAAAAAAAAAAAAAAAGdlb2dlYnJhX2phdmFzY3JpcHQuanNQSwECFAAUAAgACAA7WJxAXbaWjdwHAABWIQAADAAAAAAAAAAAAAAAAABdAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAACAAIAfgAAAHMIAAAAAA==" showResetIcon = "false" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" useBrowserForJS = "true" allowRescaling = "true" /><br />
 +
Das ist ein schiefer Drache. Die Punkte lassen sich bewegen.--[[Benutzer:Tutorin Anne|Tutorin Anne]] 11:02, 28. Apr. 2012 (CEST)

Aktuelle Version vom 28. April 2012, 10:02 Uhr

In welchen Fällen handelt es sich um eine korrekte Definition des Begriffs Parallelogramm? Begründen Sie!
1) Wenn sich in einem Viereck die Diagonalen halbieren, so ist das Viereck ein Parallelogramm.
2) Wenn in einem Drachen die gegenüberliegenden Seiten kongruent zueinander sind, so ist der Drachen ein Parallelogramm.
3) Es gibt Trapeze, die ein weiteres Paar paralleler Seiten haben und die Parallelogramme genannt werden.
4) Trapeze mit zwei zueinander kongruenten Seiten heißen Parallelogramme.


1) nicht ausreichend, da bei einem Rechteck genau das Gleiche gilt
2) in Ordnung --> es sind die Eigenschaften gegeben, dass die zwei Paare der Seiten parallel zueinander sind und gleich lang
3) in Ordnung
4) nicht ausreichend, da es eher heißen müsste: Trapeze mit zwei Paar zueinander kongruenten Seiten heißen Parallelogramme.
-- Nala23 14:04, 22. Apr. 2012
Was meinen denn die anderen dazu? Hier bietet es sich meiner Meinung nach an, auf die Lösungsvorschläge von Nala23 einzugehen und nicht nur eine weitere Lösung einzustellen.--Tutor Andreas 18:47, 22. Apr. 2012 (CEST)


Ich hätte zu 2) gasagt, dass man man diese beiden geometrischen Figuren (Drachen und Parallelogramm) nicht aufeinander beziehen kann (siehe Haus der Vierecke).


Derjenige möchte Parallelogramm definieren, dann sollte man als Oberbegriff Trapez oder Viereck/n-Eck mit n=4 benutzen.
Bei Nala23s Kommentaren zu 1) und 3) stimme ich zu.
Zu 4) hätte ich gesagt: Trapeze, bei deen die gegenüberliegenden Seiten stets parallel sind heißten Parallelogramme. --Honeydukes 23:06, 22. Apr. 2012 (CEST)
Mh? zu 1) für Rechtecke gilt das auch, das stimmt. Na und?
zu 2)und 3) überlegt nochmal...--Tutorin Anne 14:32, 24. Apr. 2012 (CEST)



Zu 4:
 Alle Parallelogramme gehören zur Klasse der Trapeze, schiefer Drachen und Vierecke. Sie sind ein Oberbegriff für Parallelogramme und können damit auch definiert werden. (vgl. Haus der Vierecke, in Didaktik der Geometrie für die Sekundarstufe 1,S.137) oder vgl. http://wikis.zum.de/geowiki/Haus_der_Vierecke_%2815.07.2011%29

Habe gerade festgestellt, dass sich meine beiden Quellen widersprechen. Sind meine Definitionen nun falsch? Oder hab ich einen Denkfehler?


1. Ein Trapez/schiefer Drachen/Viereck mit zwei Paaren paralleler Gegenseiten ist ein Parallelogramm.
 2. Ein Trapez/schiefer Drachen/Viereck mit sich gegenseitig halbierenden Diagonalen ist ein Parallelogramm.
 3. Ein Trapez/schiefer Drachen/Viereck mit einem Paar paralleler und zueinander kongruenter Seiten ist ein Parallelogramm.

 Bei Betrachtung meiner dritten Definiton fällt auf, dass sie fast der ursrünglichen entspricht - zwei konkruente Seiten sind in der Definiton gegeben, es fehlt meiner Meinung nach der Verweis auf ein paar paralleler konkruenter Seiten.--Braindead 15:26, 23. Apr. 2012 (CEST)
Ja richtig, das ist eine Möglichkeit: Deine dritte Definition verbessert Nr. 4 der Aufgabenstellung. Wenn du schreibst "Ein Viereck mit..." und dann "ein Trapez mit", dann brauchst du bei zweiterem meist weniger zusätzliche Eigenschaften nennen, da ja das Trapez schon Eigenschaften in die Definition miteinbringt. Deshalb kann man so "Trapez/schiefer Drachen/Viereck" schlecht beurteilen.--Tutorin Anne 14:32, 24. Apr. 2012 (CEST)

3) ist eine Aussage und keine Definition. Es handelt sich hier also um das selbe Problem wie in Aufgabe 1.5.--KeinKurpfälzer 20:11, 24. Apr. 2012 (CEST)

Kommentar M.G

In 3. wird behauptet, dass irgendetwas existiert. Es obliegt uns nicht mittels einer Definition festzulegen, dass etwas existiert oder nicht (wir und auch die Mathematiker sind nicht Gott oder ein anderes höheres Wesen). Wir müssen die objektive Realität so nehmen wie sie ist. Wir können den Dingen nur Namen geben und fertig. User KeinKurpfälzer hat also Recht.--*m.g.* 22:17, 24. Apr. 2012 (CEST)
Es ist nicht egal für die Definition eines Begriffs, auf welchen Oberbegriff man sich bezieht:
1. Beziehe ich mich für die Definition des Begriffs Parallelogramm auf den Oberbegriff Viereck, dann muss ich festlegen, dass unser Viereck zwei Paare paralleler Seiten hat: Wenn ein Viereck zwei Paare paralleler Seiten hat, so heißt es Parallelogramm.
2. Beziehe ich mich auf den Oberbegriff Trapez, so brauche ich nur ein weiteres Paar paralleler Seiten zu fordern, denn jedes Trapez hat ja bereits ein solches: Wenn ein Trapez ein weiteres Paar zueinander paralleler Seiten besitzt, so heißt es Parallelogramm.
3. Will ich den relativ selten verwendeten Oberbegriff schiefer Drachen verwenden, so macht es Sinn, zunächst die Definition für den Begriff schiefer Drachen zu betrachten: Wenn eine Diagonale eines Vierecks die andere Diagonale dieses Vierecks halbiert, so ist das Viereck eine schiefer Drachen. In jedem Parallelogramm halbieren sich die Diagonalen gegenseitig. Also gibt es in jedem Parallelogramm eine Diagonale , die die halbiert: Jedes Parallelogramm ist somit ein schiefer Drachen. 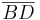Das Besondere eines jeden schiefen Drachens, der auch als Parallelogramm bezeichnet werden darf ist, dass in einem solchen schiefen Drachen nicht nur die eine Diagonale die andere sondern auch die andere die eine Diagonale halbiert (meint sie halbieren einender gegenseitig): Es sei \overline{ABCD} ein schiefer Drachen, wobei die Diagonale \overline{AC} die Diagonale \overline{BD} halbieren möge. 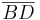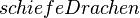Wenn auch die Diagonale \overline{BD} die Diagonale \overline{AC} halbiert, so heißt der schiefe Drachen \overline{ABCD} Parallelogramm.--*m.g.* 22:17, 24. Apr. 2012 (CEST)


Frage zur Definition schiefer Drachen in 3.: Wo halbieren sich die Diagonalen in einem schiefen Drachen?--Braindead 09:51, 25. Apr. 2012 (CEST)


Das ist ein schiefer Drache. Die Punkte lassen sich bewegen.--Tutorin Anne 11:02, 28. Apr. 2012 (CEST)

Von „http://geometrie.zum.de/index.php?title=Lösung_von_Aufgabe_1.6_(SoSe_12)&oldid=12407“