Lösung von Aufgabe 3.5 S (SoSe 12): Unterschied zwischen den Versionen

Version vom 3. Mai 2012, 19:09 Uhr

Aufgabe 3.5

Das Parallelenaxiom lautet wie folgt:
Zu jeder Geraden g und zu jedem nicht auf g liegenden Punkt A gibt es höchstens eine Gerade, die durch A verläuft und zu g parallel ist.
Nutzen Sie dieses Axiom, beim Lösen der folgenden Aufgabe:
Es seien a, b und c drei paarweise verschiedene Geraden in ein und derselben Ebene.
a) Beweisen Sie folgende Implikation durch einen Widerspruchsbeweis: .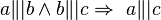
b) Welche Eigenschaft der Relation auf der Menge aller Geraden einer Ebene haben Sie hiermit gezeigt?

Lösungsvorschlag 1

a)
Voraussetzung: a,b,c sind paarweise verschiedene Geraden

Behauptung: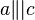

Annahme: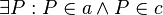

Beweis:
(1) 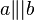Voraussetzung
(2) 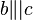Voraussetzung
(3) 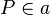Annahme (Parallelenaxiom Schnittpunkt mit a)
(4) 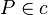Annahme (Parallelenaxiom Schnittpunkt mit c)
(5) 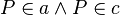(3),(4) da Punkt P sowohl auf a, als auch auf c liegt ist das ein Widerspruch zur Voraussetzung. --Goliath 17:03, 3. Mai 2012 (CEST)

• Der Beweis ist meiner Meinung nach noch nicht richtig, denn du hast keinen Widerspruch zur VSS (a,b,c sind paarweise verschiedene Geraden). Vielleicht hast du auch die richtige Idee und es ist nur beim Niederschreiben verloren gegangen... --Tutor Andreas 18:25, 3. Mai 2012 (CEST)

Meine Idee war: Laut dem Parallelenaxiom gibt es doch höchstens eine Gerade, die durch den Punkt A läuft und zu g parallel ist. Ich dachte nun, dass doch in (5) gezeigt wäre, dass sowohl a als auch c durch P gehen und sie deshalb laut (5) nicht parallel sein können. Die Voraussetzung besagt doch, dass 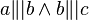und dann doch auch Fehler beim Parsen(Syntaxfehler): \\ a \|| c\

und da dachte ich, dass in (5) gezeigt wäre, dass a und c in dem Fall nicht parallel sein können. Und das wäre dann mein Widerspruh zur Voraussetzung. Bin ich da komplett auf dem falschen Dampfer, oder hab ich es einfach falsch aufgeschrieben?????--Goliath 18:35, 3. Mai 2012 (CEST)

• Wie du schon sagst, gibt es laut dem Parallelenaxiom höchstens eine Gerade, die durch A geht und parallel zu g (ich denke du meinst b) verläuft, aber das heißt nciht, dass a und c nicht parallel sein können. Und da ist noch etwas. Du hast im letzten Beitrag geschrieben, dass "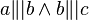und dann doch auch Fehler beim Parsen(Syntaxfehler): \\ a \|| c\

", aber Fehler beim Parsen(Syntaxfehler): \\ a \|| c\

ist deine Behauptung und nicht die VSS. --Tutor Andreas 18:53, 3. Mai 2012 (CEST)

b) Hiermit wurde die Transitivität gezeigt.--Goliath 17:17, 3. Mai 2012 (CEST)

Lösungsvorschlag 2

a) Wenn a parallel zu b ist und b parallel zu c, dann ist auch a parallel zu c.

Voraussetzung: Fehler beim Parsen(Lexikalischer Fehler): \ a \|| b \wedge b \|| c \

Behauptung: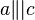

Beweis durch Widerspruch, daher ist es ein indirekter Beweis: es ist zu zeigen, dass die Negation der Behauptung nicht gilt. Dabei wird angenommen, dass die Behauptung nicht gilt. Dadurch wird der Widerspruch erzeugt!

Annahme: 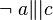(a ist nicht parallel zu c. Wie kann ich das "nicht parallel" besser darstellen?)--Braindead 19:46, 3. Mai 2012 (CEST)