Streckenantragen oder das Axiom vom Lineal: Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: == Der Mittelpunkt einer Strecke== Wir wissen nun, dass eine offene Strecke <math>\overline{AB}</math> die Menge aller Punkte ist, die zwischen <math>\ A</math> und <ma...) |
*m.g.* (Diskussion | Beiträge) (→Der Mittelpunkt einer Strecke) |
||
| Zeile 4: | Zeile 4: | ||
===== Definition III.1: (Mittelpunkt einer Strecke) ===== | ===== Definition III.1: (Mittelpunkt einer Strecke) ===== | ||
::Wenn der Punkt <math>\ M</math> der Strecke <math>\overline{AB}</math> zu den Endpunkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand hat, so heißt er Mittelpunkt der Strecke <math>\overline{AB}</math>. | ::Wenn der Punkt <math>\ M</math> der Strecke <math>\overline{AB}</math> zu den Endpunkten <math>\ A</math> und <math>\ B</math> ein und denselben Abstand hat, so heißt er Mittelpunkt der Strecke <math>\overline{AB}</math>. | ||
| + | |||
| + | (Hinweis: Diskutieren Sie den bestimmten Artikel in Definition III.1) | ||
| + | |||
| + | Was das Definieren angeht, werden wir langsam vorsichtig. Definieren dürfen wir alles was wir wollen. Wir müssen uns dann allerdings die Frage nach Sinn und Korrektheit unserer Definition gefallen lassen. von beidem dürften wir bezüglich Definition III.1 überzeugt sein, weshalb wir voller Überzeugung den folgenden Satz formulieren: | ||
| + | |||
| + | ===== Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke) ===== | ||
| + | ::Jede Strecke hat genau einen Mittelpunkt. | ||
Version vom 31. Mai 2010, 11:04 Uhr
Der Mittelpunkt einer Strecke
Wir wissen nun, dass eine offene Strecke 
die Menge aller Punkte ist, die zwischen 
und 
liegen. Vereinigt man diese Menge mit der Menge der beiden Endpunkte und , so hat man die gesamte Strecke . Zu unseren grundlegenden Vorstellungen von Strecken gehört, dass jede Strecke einen Mittelpunkt 
hat. wäre der Punkt auf , der sowohl zu als auch zu denselben Abstand 
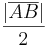hat.
Definition III.1: (Mittelpunkt einer Strecke)
- Wenn der Punkt der Strecke zu den Endpunkten und ein und denselben Abstand hat, so heißt er Mittelpunkt der Strecke .
- Wenn der Punkt
(Hinweis: Diskutieren Sie den bestimmten Artikel in Definition III.1)
Was das Definieren angeht, werden wir langsam vorsichtig. Definieren dürfen wir alles was wir wollen. Wir müssen uns dann allerdings die Frage nach Sinn und Korrektheit unserer Definition gefallen lassen. von beidem dürften wir bezüglich Definition III.1 überzeugt sein, weshalb wir voller Überzeugung den folgenden Satz formulieren:
Satz III.1: (Existenz und Eindeutigkeit des Mittelpunkte einer Strecke)
- Jede Strecke hat genau einen Mittelpunkt.
