Lösung von Aufgabe 3.4 S (SoSe 12): Unterschied zwischen den Versionen
(→Aufgabe 3.4) |
|||
| Zeile 18: | Zeile 18: | ||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
| − | Beweis durch Widerspruch, d.h. A | + | Beweis durch Widerspruch, d.h. <math>A \wedge \neg B</math> (Hilfe bei Formelschreibweise!) |
| − | Vor.: |AC|< |BC| < |AB| | + | Vor.: |AC|< |BC| < |AB|<br /> |
| − | Beh.: |α| ≠ |β| | + | Beh.: |α| ≠ |β|<br /> |
| − | Annahme: |AC|< |BC| < |AB| und |α| = |β| | + | Annahme: |AC|< |BC| < |AB| und |α| = |β|<br /> |
| − | Beweis: (1) | + | Beweis: <br /> |
| + | (1)Wenn |α| = |β|, dann ist |AC|= |BC| [vgl. Umkehrung des Basiswinkelsatzes]<br /> | ||
| + | (2)|AC|= |BC| ist ein Widerspruch zur Voraussetzung! q.e.d | ||
Version vom 22. Mai 2012, 12:28 Uhr
Vorlage:Zitat wpde==Aufgabe 3.4==
Satz: In einem Dreieck 
mit |AC|< |BC| < |AB| sind die Winkel α und β nicht kongruent zueinander.
a) Welcher Beweis ist korrekt? Begründen Sie ausführlich! (Der Basiswinkelsatz und seine Umkehrung seien bereits bewiesen.)
Beweis 1)
Sei ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Da nach Voraussetzung |AC| ≠ |BC| gilt nach dem Basiswinkelsatz |α| ≠ |β|. Damit ist der Satz bewiesen.
Beweis 2)
Sei ein Dreieck.
Vor: |AC|< |BC| < |AB|.
Beh: |α| ≠ |β|
Bew: Nach Umkehrung des Basiswinkelsatzes gilt: Wenn |α|= |β| dann gilt |AC|= |BC|. Die Kontraposition der Umkehrung lautet also: Wenn |AC| ≠ |BC| dann gilt |α| ≠ |β|. Da die Kontraposition gleichwertig ist, kann man auch diese beweisen. Da nach Voraussetzung gilt: |AC|< |BC|, d.h. |AC| ≠ |BC|, kann nach Kontraposition der Umkehrung des Basiswinkelsatzes direkt gefolgert werden: |α| ≠ |β|. Damit ist der Satz bewiesen.
b) Beweisen Sie den Satz indirekt mit Widerspruch.
Beweis durch Widerspruch, d.h.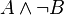 
(Hilfe bei Formelschreibweise!)
Vor.: |AC|< |BC| < |AB|
Beh.: |α| ≠ |β|
Annahme: |AC|< |BC| < |AB| und |α| = |β|
Beweis:
(1)Wenn |α| = |β|, dann ist |AC|= |BC| [vgl. Umkehrung des Basiswinkelsatzes]
(2)|AC|= |BC| ist ein Widerspruch zur Voraussetzung! q.e.d
