Lösung von Zusatzaufgabe 5.2 (SoSe 12): Unterschied zwischen den Versionen
Nemo81 (Diskussion | Beiträge) |
*m.g.* (Diskussion | Beiträge) |
||
| Zeile 1: | Zeile 1: | ||
| + | ==Die Aufgabe= | ||
Beweisen Sie Satz I.7 : Jede Ebene enthält (wenigstens) drei Punkte.<br /><br /> | Beweisen Sie Satz I.7 : Jede Ebene enthält (wenigstens) drei Punkte.<br /><br /> | ||
| − | |||
| + | ==Lösungsvorschlag von Nemo81== | ||
| + | ===Der Vorschlag=== | ||
Vor. Ebene E1 | Vor. Ebene E1 | ||
| Zeile 14: | Zeile 16: | ||
2) A,B,C elemt E1 laut Ax I/4 q.e.d | 2) A,B,C elemt E1 laut Ax I/4 q.e.d | ||
--[[Benutzer:Nemo81|Nemo81]] 15:52, 30. Mai 2012 (CEST) | --[[Benutzer:Nemo81|Nemo81]] 15:52, 30. Mai 2012 (CEST) | ||
| + | ===Bemerkungen von M.G.=== | ||
| + | ====Zur Voraussetzung==== | ||
| + | Besser: | ||
| + | |||
| + | Es sei <math>E_1</math> eine Ebene. | ||
| + | |||
| + | oder: | ||
| + | |||
| + | Wir gehen davon aus, dass <math>E_1</math> eine Ebene ist. | ||
| + | |||
| + | Nur so Ebene <math>E_1</math> klingt nicht so gut. | ||
| + | |||
| + | ====Zur Behauptung==== | ||
| + | Besser: | ||
| + | |||
| + | Wir haben zu zeigen, dass es drei paarweise verschiedene Punkte <math>A,B,C</math> gibt, die zu <math>E_1</math> gehören. | ||
| + | |||
| + | Jede Behauptung ist eine Aussage für sich. Sie behaupten <math>A,B,C \in E_1</math>. Was ist das für eine Behauptung? Wir wissen durch die Formulierung <math>A,B,C \in E_1</math> nicht wirklich worum es geht. Welche drei Punkte <math>A, B, C</math>? Ihre Behauptung kann keinen Wahrheitsgehalt haben, da wir nicht wisse, um was für Punkte es geht. Letztlich ist unsere Behauptung eine Existenzaussage. Es gibt drei Punkte , die zur Ebene <math>E_1</math> gehören. | ||
| + | |||
| + | ====Zum besseren Verständnis, der Satz noch mal in Wenn-Dann==== | ||
| + | |||
| + | Wenn (die Punktmenge) <math>E_1</math> eine Ebene ist, dann gibt es wnigstens drei parweise verschiedene Punkte, die zu <math>E_1</math> gehören. | ||
| + | [[Category:Einführung_S]] | ||
Version vom 3. Juni 2012, 16:46 Uhr
Inhaltsverzeichnis[Verbergen] |
=Die Aufgabe
Beweisen Sie Satz I.7 : Jede Ebene enthält (wenigstens) drei Punkte.
Lösungsvorschlag von Nemo81
Der Vorschlag
Vor. Ebene E1
Beh: A,B,C element E1
Bew:
1) E1 laut Vor.
2) A,B,C elemt E1 laut Ax I/4 q.e.d
--Nemo81 15:52, 30. Mai 2012 (CEST)
Bemerkungen von M.G.
Zur Voraussetzung
Besser:
Es sei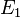 
eine Ebene.
oder:
Wir gehen davon aus, dass 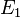eine Ebene ist.
Nur so Ebene 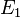klingt nicht so gut.
Zur Behauptung
Besser:
Wir haben zu zeigen, dass es drei paarweise verschiedene Punkte 
gibt, die zu 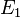gehören.
Jede Behauptung ist eine Aussage für sich. Sie behaupten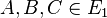 
. Was ist das für eine Behauptung? Wir wissen durch die Formulierung 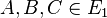nicht wirklich worum es geht. Welche drei Punkte ? Ihre Behauptung kann keinen Wahrheitsgehalt haben, da wir nicht wisse, um was für Punkte es geht. Letztlich ist unsere Behauptung eine Existenzaussage. Es gibt drei Punkte , die zur Ebene 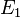gehören.
Zum besseren Verständnis, der Satz noch mal in Wenn-Dann
Wenn (die Punktmenge) 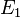eine Ebene ist, dann gibt es wnigstens drei parweise verschiedene Punkte, die zu 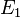gehören.
