Übung Aufgaben 6 P (SoSe 12): Unterschied zwischen den Versionen
(→Aufgabe 6.2) |
(→Aufgabe 6.1) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
[[Lösung von Aufgabe 6.1P (SoSe_12)]] | [[Lösung von Aufgabe 6.1P (SoSe_12)]] | ||
| − | |||
==Aufgabe 6.2== | ==Aufgabe 6.2== | ||
| Zeile 10: | Zeile 9: | ||
[[Lösung von Aufgabe 6.2P (SoSe_12)]] | [[Lösung von Aufgabe 6.2P (SoSe_12)]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Aufgabe 6.3== | ==Aufgabe 6.3== | ||
Aktuelle Version vom 5. Juni 2012, 11:40 Uhr
Inhaltsverzeichnis |
Aufgabe 6.1
Beweisen Sie: Aus 
folgt 
.
Lösung von Aufgabe 6.1P (SoSe_12)
Aufgabe 6.2
Beweisen Sie: Es sei mit 
sind paarweise verschieden.
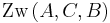Dann gilt genau eine der folgenden Zwischenrelationen: oder 
oder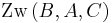 
.
Lösung von Aufgabe 6.2P (SoSe_12)
Aufgabe 6.3
Es seien A und B zwei verschiedene Punkte. Welche Ergebnisse erzielen Sie nach den folgenden Mengenoperationen?
a)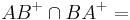 
b)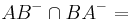 
c) 
geschnitten mit dem Kreis um 
durch 
=
d)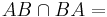
Lösung von Aufgabe 6.3P (SoSe_12)
Aufgabe 6.4
Beweisen Sie den Satz von Pasch. Verwenden Sie für den Beweis die Definition von Halbebenen und gehen Sie davon aus, dass jede Ebene in genau zwei Halbebenen geteilt werden kann.
Lösung von Aufgabe 6.4P (SoSe_12)
Aufgabe 6.5
Gegeben seien drei paarweise verschiedene und kollineare Punkte A, B und C in einer Ebene E. Ferner sei eine Gerade g Teilmenge der Ebene E, wobei keiner der Punkte A, B und C auf g liegen möge. Beweisen Sie folgenden Zusammenhang:
