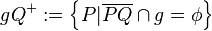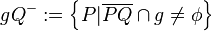Lösung von Aufgabe 6.4P (SoSe 12)

Beweisen Sie den Satz von Pasch. Verwenden Sie für den Beweis die Definition von Halbebenen und gehen Sie davon aus, dass jede Ebene in genau zwei Halbebenen geteilt werden kann.
ist es nicht auch ein axiom?--Studentin 16:10, 27. Mai 2012 (CEST)

• Man kann die Geometrie so aufbauen, dass der Satz von Pasch kein Satz sondern ein Axiom ist. Das ist möglich.
  
• Es geht aber genauso auch anders, denn es gibt eine äquivalente Aussage. Diese besagt eben, dass jede Ebene in genau zwei Halbebenen geteilt werden kann.--Tutorin Anne 17:17, 27. Mai 2012 (CEST)
  

indirekter Beweis

Wer versucht sich?
Wer möchte kann die Tabelle zur Hilfe nehmen:

Voraussetzung	(V. hier eintragen)
Behauptung	(Beh. hier eintragen)
Annahme	(A. hier eintragen)

Beweisschritt	Begründung
1 (Schritt 1)	(Begründung 1)
2 (Schritt 2)	(Begründung 2)
3 (Schritt)	(Begründung)
4 (Schritt)	(Begründung)

--Tutorin Anne 16:02, 6. Jun. 2012 (CEST)

direkter Beweis

okay, ich kopier mir mal alles rein, was ich brauchen könnte, um alles beisammen zu haben. erst die definitionen der offenen halbebenen:

Definition II.1: (offene Halbebene)

Es sei $\ \varepsilon$ eine Ebene in der die Gerade $\ g$ liegen möge. Ferner sei $\ Q$ ein Punkt der Ebene $\ \varepsilon$, der nicht zur Geraden $\ g$ gehört.
Unter den offenen Halbebenen $\ gQ^{+}$ und $\ gQ^{-}$ bezüglich der Trägergeraden $\ g$ versteht man die folgenden Teilmengen der Ebene $\ \varepsilon$ ohne die Gerade $\ g$ :

$\ gQ^{+}:= \left\{ {P|\overline{PQ} \cap g=\phi } \right\}$

$\ gQ^{-}:= \left\{ {P|\overline{PQ} \cap g\neq\phi } \right\}$

dann den satz von pasch, den wir hier beweisen sollen:
Satz II.1: Der Satz von Pasch

Gegeben sei ein Dreieck $\overline{ABC}$. Ferner sei $\ g$ eine Gerade, die durch keinen der drei Eckpunkte $\ A, B, C$ geht. Wenn $\ g$ eine der drei Seiten des Dreiecks $\overline{ABC}$ schneidet, dann schneidet $\ g$ genau eine weitere Seite des Dreiecks $\overline{ABC}$.

desweiteren sollen wir davon ausgehen, dass jede ebene in genau zwei halbebenen geteilt werden kann - wahrscheinlich mit betonung auf "genau", also zwei und nicht nur eine, drei oder mehr halbebenen.


so, wir haben also eine ebene e, in der eine gerade g liegt.
außerdem liegt in der ebene e ein punkt q, dieser darf nicht auf der geraden g liegen.
um die offenen halbebenen bezgl. der geraden g zu erhalten, betrachten wir beliebige punkte p und schauen, ob die strecken pq die gerade g schneiden oder nicht und kommen dadurch zu offenen halbebenen gq+ und gq-.
im satz von pasch haben wir das dreieck abd gegeben und eine gerade g, die durch keinen der drei eckpunkte geht
(in welchen fällen gehen wir eigentlich davon aus, dass wir und in einer ebene befinden und wann nicht???)

jetzt zur eigentlichen aufgabe:

voraussetzung: g schneidet einer der drei seiten des dreicks abc
hehauptung: g schneidet genau eine weitere seite des dreiecks abc

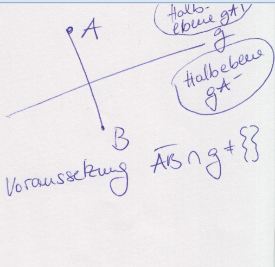
ich nehme mir nur den punkt a, um die ebene in zwei halbebenen ga+ und ga- zu teilen ich versuche nun den beweis, wenn g als beispiel die seite ab schneidet. (als voraussetzung)

dann muss (laut behauptung) g entweder die seite ac oder die seite bc schneiden (also kein "mathe-oder" was soviel wie und/oder bedeutet, sondern ein wirkliches "entweder-oder" (nur ab oder ac wird geschnitten))
der dritte punkt c liegt ja in der gleichen ebene e und nicht auf der geraden g.
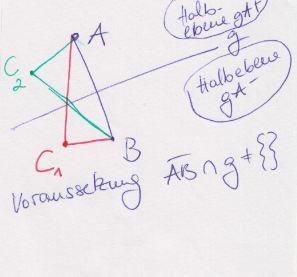
da wir nur die beiden halbebenen zur verfügung haben, kann der punkt c entweder auf der halbebene liegen, auf der auch punkt a (ga+) liegt, oder auf der halbebene, auf der der punkt a nicht liegt (ga-).

liegt punkt c auf ga- (in meiner zeichnung rot), dann schneidet laut unserer def. der halbebenen auch ac die gerade g, nicht aber die seite ab.
umgekehrt, wenn c auf der halbebene ga+ liegt (grüne zeichnung): dann schneidet laut unserer def. der halbebenendie seite ac nicht die gerade g, g wird dagegen von bc geschnitten.
damit stimmt der satz von pasch.
jetzt müsste ich wahrscheinlich das gleiche nochmals für den fall machen, dass die voraussetzung eine andere ist (die gerade g schneidet nicht ab, sondern ac oder bc), oder?
--Studentin 16:00, 3. Jun. 2012 (CEST)
Sehr gut gezeigt! Du kannst schreiben, dass der Beweis für den anderen Fall analog ist und musst ihn somit nicht nochmal aufschreiben. --Tutorin Anne 16:02, 6. Jun. 2012 (CEST)

nochmal meine frage von der übung:
geht es auch in der art bei der klausur oder muss es in tabellenform sein?--Studentin 17:20, 6. Jun. 2012 (CEST)
Nein, so wie du es machst ist es völlig in Ordnung. Tabelle muss nicht sein. Sie hilft lediglich, dass man die Übersicht behält und nicht Beweisschritte nennt ohne diese zu begründen.--Tutorin Anne 23:04, 6. Jun. 2012 (CEST)