Übung 7: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.1) |
*m.g.* (Diskussion | Beiträge) (→Aufgabe 7.2) |
||
| Zeile 4: | Zeile 4: | ||
== Aufgabe 7.2 == | == Aufgabe 7.2 == | ||
Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right|</math> und <math>\overline{AB^{*}} \subset \overline{AB}</math>. | Beweisen Sie: Zu jeder Strecke <math>\overline{AB}</math> existiert genau eine Strecke <math>\overline{AB^{*}}</math> mit <math>\left| AB^{*} \right| = \frac{1}{\pi} \left| AB \right|</math> und <math>\overline{AB^{*}} \subset \overline{AB}</math>. | ||
| + | |||
| + | == Aufgabe 7.3 == | ||
| + | Der Punkt <math>\ B</math> möge die Strecke <math>\overline{AC}</math> derart in die Teilstrecken <math>\overline{AB}</math> und <math>\overline{BC}</math> teilen, dass <math>\left| AB \right| > \left| BC \right|</math> gilt. Beweisen Sie:<br /> | ||
| + | Wenn <math>\frac{ \left| AC \right| }{\left| AB \right| } = \frac{\left| AB \right| }{\left| BC \right| }</math> | ||
Version vom 3. Juni 2010, 12:20 Uhr
Aufgabe 7.1
Beweisen Sie: Zu jeder Strecke 
existiert genau eine Strecke 
mit 
und 
.
Aufgabe 7.2
Beweisen Sie: Zu jeder Strecke existiert genau eine Strecke mit 
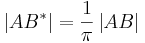und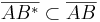 
.
Aufgabe 7.3
Der Punkt 
möge die Strecke 
derart in die Teilstrecken und 
teilen, dass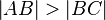 
gilt. Beweisen Sie:
Wenn 
