Definitionsversuche V3: Unterschied zwischen den Versionen
K (→Bemerkung M.G.) |
*m.g.* (Diskussion | Beiträge) (→Bemerkung M.G.) |
||
| Zeile 22: | Zeile 22: | ||
<br />Ja genau.. d.h. ich könnte es folgendermaßen formulieren: <br /> | <br />Ja genau.. d.h. ich könnte es folgendermaßen formulieren: <br /> | ||
* das Innere der Winkel liegt bezüglich dieser beiden Geraden jeweils in einer anderen Halbebene.<br /> | * das Innere der Winkel liegt bezüglich dieser beiden Geraden jeweils in einer anderen Halbebene.<br /> | ||
| − | Oder muss das Innere eines Winkels dann auch noch definiert werden?--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:17, 16. Jun. 2012 (CEST) | + | Oder muss das Innere eines Winkels dann auch noch definiert werden?--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 21:17, 16. Jun. 2012 (CEST)<br /> |
| + | Das Innere eines Winkels hatten wir schon definiert. Es ist hier also nicht notwendig, noch mal das Innere zu definieren.--[[Benutzer:*m.g.*|*m.g.*]] 16:11, 18. Jun. 2012 (CEST) | ||
---- | ---- | ||
zurück zu: | zurück zu: | ||
[[Winkel SS 2012]] | [[Winkel SS 2012]] | ||
[[Kategorie: Einführung_S]] | [[Kategorie: Einführung_S]] | ||
Aktuelle Version vom 18. Juni 2012, 15:11 Uhr
Inhaltsverzeichnis |
Definition Scheitelwinkel
(Definition V.3)
Definitionen von Nummero6/Tchu Tcha Tcha
Definitionsversuch 1
Definition
(Scheitelwinkel)
- Zwei Winkel bilden ein Paar von Scheitelwinkeln, wenn gilt:
- Winkel 1:
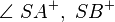
- Winkel 2:
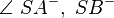
- Zwei Winkel bilden ein Paar von Scheitelwinkeln, wenn gilt:
Bemerkung M.G.
Vielleicht sollten wir noch ausschließen, dass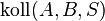 
gelten kann. Ansonsten korrekt.--*m.g.* 17:21, 16. Jun. 2012 (CEST)
Definitionsversuch 2
Definition
(Scheitelwinkel)
Zwei Winkel bilden ein Paar von Scheitelwinkeln, wenn sie einen gemeinsamen Scheitelpunkt haben und für jeden Winkel gilt:
- jeweils beide Schenkel sind Teilmenge von genau 2 Geraden und
- jeder Winkel liegt bezüglich dieser beiden Geraden in einer anderen Halbebene
--Tchu Tcha Tcha 20:47, 10. Jun. 2012 (CEST)
Bemerkung M.G.
- jeder Winkel liegt bezüglich dieser beiden Geraden in einer anderen Halbebene:
Das ist so nicht ganz korrekt. Sie meinen das Innere der Winkel.--*m.g.* 17:24, 16. Jun. 2012 (CEST)
Ja genau.. d.h. ich könnte es folgendermaßen formulieren:
- das Innere der Winkel liegt bezüglich dieser beiden Geraden jeweils in einer anderen Halbebene.
Oder muss das Innere eines Winkels dann auch noch definiert werden?--Tchu Tcha Tcha 21:17, 16. Jun. 2012 (CEST)
Das Innere eines Winkels hatten wir schon definiert. Es ist hier also nicht notwendig, noch mal das Innere zu definieren.--*m.g.* 16:11, 18. Jun. 2012 (CEST)
zurück zu: Winkel SS 2012
