Lösung von Aufgabe 7.1 S (SoSe 12): Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
Lösungsvorschlag: | Lösungsvorschlag: | ||
| − | a) AB+ | + | a) AB<sup>+</sup> <math>\cap</math> BA<sup>+</sup> = <math>\overline {AB}</math><br /> |
| − | b) AB- | + | b) AB<sup>-</sup> <math>\cap</math> BA<sup>-</sup> = {}<br /> |
c) AB geschnitten mit dem Kreis um A durch B = B,X und |AX| = |AB| (man sollte noch ergänzen, dass X auf AB liegt und X <math>X \neq B</math> gilt.--[[Benutzer:Andreas|Tutor Andreas]] 12:36, 19. Jun. 2012 (CEST)<br /> | c) AB geschnitten mit dem Kreis um A durch B = B,X und |AX| = |AB| (man sollte noch ergänzen, dass X auf AB liegt und X <math>X \neq B</math> gilt.--[[Benutzer:Andreas|Tutor Andreas]] 12:36, 19. Jun. 2012 (CEST)<br /> | ||
| − | d) AB | + | d) AB <math>\cap</math> BA = AB (AB und BA sind identisch)<br /> |
| − | |||
--[[Benutzer:RitterSport|RitterSport]] 19:07, 9. Jun. 2012 (CEST) | --[[Benutzer:RitterSport|RitterSport]] 19:07, 9. Jun. 2012 (CEST) | ||
Version vom 19. Juni 2012, 12:40 Uhr
Lösungsvorschlag:
a) AB+ 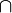 BA+ =
BA+ = 
b) AB- 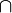 BA- = {}
BA- = {}
c) AB geschnitten mit dem Kreis um A durch B = B,X und |AX| = |AB| (man sollte noch ergänzen, dass X auf AB liegt und X 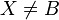 gilt.--Tutor Andreas 12:36, 19. Jun. 2012 (CEST)
gilt.--Tutor Andreas 12:36, 19. Jun. 2012 (CEST)
d) AB 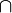 BA = AB (AB und BA sind identisch)
BA = AB (AB und BA sind identisch)
--RitterSport 19:07, 9. Jun. 2012 (CEST)
a) = Strecke AB b) Alle Punkte außer die Strecke, also die leere Menge. ={ } c) Da Punkt A nicht Element seines eigenen Kreises ist, ist die Menge leer. = { } d) = {A,B} --Luca123 20:00, 10.Jun. 2012 (CEST)
Dito
Außer bei
c) {B}
Strecke AB ist der kreisradius somit ist B in beiden enthalten
Gedanke Nummero6/Tchu Tcha Tcha:
Ich gebe RitterSport meine Stimme ;-)
Bsp. für c):
--Tchu Tcha Tcha 15:59, 12. Jun. 2012 (CEST)
__________________________________________________________________________________________________
_____________________________________
Was soll man da noch sagen. Wieder was gelernt!
--Luca12323:31, 14.Jun. 2012 (CEST)

