Lösung von Aufgabe 2.6 S (SoSe 12): Unterschied zwischen den Versionen
*m.g.* (Diskussion | Beiträge) (→Zweiter Versuch von Goliath) |
K (→Aufgabe 2.6) |
||
| (4 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 20: | Zeile 20: | ||
| − | 2. Wenn ein Dreieck rechtwinklig ist, dann liegt der Mittelpunkt seines Umkreises auf der Hypothenuse dieses Dreiecks.--[[Benutzer:Oz44oz|Oz44oz]] 20:09, 28. Apr. 2012 (CEST) | + | 2. Wenn ein Dreieck rechtwinklig ist, dann liegt der Mittelpunkt seines Umkreises auf der Hypothenuse dieses Dreiecks.--[[Benutzer:Oz44oz|Oz44oz]] 20:09, 28. Apr. 2012 (CEST)<br />Unsere Lerngruppe ist derselben Meinung..--[[Benutzer:Nummero6|Tchu Tcha Tcha]] 13:32, 19. Jun. 2012 (CEST) |
| Zeile 78: | Zeile 78: | ||
Jetzt ist es völlig korrekt.--[[Benutzer:*m.g.*|*m.g.*]] 23:05, 2. Mai 2012 (CEST) | Jetzt ist es völlig korrekt.--[[Benutzer:*m.g.*|*m.g.*]] 23:05, 2. Mai 2012 (CEST) | ||
| + | |||
| + | @M.G. JUHU, jetzt hab ich es auch verstanden! --[[Benutzer:Goliath|Goliath]] 14:46, 3. Mai 2012 (CEST) | ||
| + | |||
[[Category:Einführung_S]] | [[Category:Einführung_S]] | ||
| + | |||
| + | ====Grundsätzliches==== | ||
| + | Eine mir vor allem auch für die Klausur wichtig erscheinende Frage ist, ob es Signal-Wörter gibt, die in eine Richtung der Implikation deuten. | ||
| + | Gerade beim letzten Beispiel waren wir uns nicht ganz einig, ob "Wenn es ein Dreieck ist, dann beträgt die Winkelsumme 180°." oder "Wenn die Winkelsumme 180° beträgt, dann handelt es sich um ein Dreieck." die Implikation oder deren Umkehrung ist. | ||
| + | Die Argumentationslinien sind einmal, dass man zuerst auf die Winkelsumme trifft (und in diesem Falle das Dreieck erst am Ende des Satzes genannt werden würde), andererseits dass das Dreieck das eigentlich Beherrschende des Satzes ist. | ||
| + | Mir ist klar, dass es für die Aussage eigentlich unerheblich ist, da es sich um eine Äquivalenz handelt. Trotzdem fände ich es interessant, was denn jetzt die Umkehrung ist und was nicht. --[[Benutzer:Mathen00b|Mathen00b]] 13:00, 3. Mai 2012 (CEST) | ||
Aktuelle Version vom 19. Juni 2012, 12:32 Uhr
Inhaltsverzeichnis |
Aufgabe 2.6
Bringen Sie die folgenden Implikationen in die Form Wenn-Dann:
- Jedes Quadrat hat vier rechte Innenwinkel.
- Der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks liegt auf der Hypotenuse dieses Dreiecks.
- In einem konvexen Viereck schneiden sich die Diagonalen des Vierecks.
- Die Geraden, die durch die Diagonalen einer Raute
 eindeutig bestimmt sind, sind Symmetrieachsen von
eindeutig bestimmt sind, sind Symmetrieachsen von  .
.
- Es sei
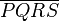 ein Paralellogramm. Es gilt:
ein Paralellogramm. Es gilt: 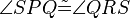 .
.
- Die Innenwinkelsumme im Dreieck beträgt 180°.
1. Wenn  ein Quadrat ist, dann hat es vier rechte Innenwinkel.
ein Quadrat ist, dann hat es vier rechte Innenwinkel.
2. Wenn der Mittelpunkt des Umkreises eines rechtwinkligen Dreiecks bestimmt wird, dann liegt dieser auf der Hypothenuse dieses Dreiecks.
3. Wenn ein Viereck konvex ist, dann schneiden sich seine Diagonalen.
4. Wenn die Diagonalen einer Raute  durch Geraden eindeutig bestimmt sind, dann sind dies Symmetrieachsen von
durch Geraden eindeutig bestimmt sind, dann sind dies Symmetrieachsen von  .
.
5. Wenn 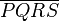 ein Paralellogramm ist, dann sind seine Winkel
ein Paralellogramm ist, dann sind seine Winkel 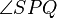 und
und 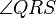 konkruent zueinander.
konkruent zueinander.
6. Wenn  ein Dreieck ist, dann beträgt seine Innenwinkelsumme 180°.
ein Dreieck ist, dann beträgt seine Innenwinkelsumme 180°.
von Wehnerj
Wehnerj - bitte immer dein Kürzel hinter deine Beiträge schreiben, damit man sich darauf beziehen kann.
Das sind gut und weniger gute Formulierungen dabei, was meinen die anderen?--Tutorin Anne 10:44, 28. Apr. 2012 (CEST)
- Ich habe mal ein paar mathematische Schreibweisen eingefügt, damit ihr sehen könnt, wie diese in LaTex geschrieben werden. Hier ist die Seite, auf der man alles nachlesen kann ZUM-Wiki Hilfe zu LaTeX--Tutor Andreas 16:05, 29. Apr. 2012 (CEST)
2. Wenn ein Dreieck rechtwinklig ist, dann liegt der Mittelpunkt seines Umkreises auf der Hypothenuse dieses Dreiecks.--Oz44oz 20:09, 28. Apr. 2012 (CEST)
Unsere Lerngruppe ist derselben Meinung..--Tchu Tcha Tcha 13:32, 19. Jun. 2012 (CEST)
4.Wenn ein Viereck eine Raute ist, dann sind beide Diagonalen Symmetrieachsen.
5. Wenn ein Viereck ein Paralellogramm ist, dann sind die gegenüberliegenden Winkel gleich groß.
6. Wenn das Vieleck ein Dreieck ist, dann beträgt die Innenwinkelsumme 180. --Oz44oz 22:32, 1. Mai 2012 (CEST)
4. Wenn die Diagonalen einer Raute  die Geraden eindeutig bestimmen, dann sind die Geraden Symmetrieachsen von
die Geraden eindeutig bestimmen, dann sind die Geraden Symmetrieachsen von  .--Goliath 13:38, 29. Apr. 2012 (CEST)
.--Goliath 13:38, 29. Apr. 2012 (CEST)
@M.G. Neuer Versuch:
4. Wenn die Diagonalen einer Raute  durch die Strecken der Eckpunkte eindeutig bestimmt sind, dann sind es Symmetrieachsen von
durch die Strecken der Eckpunkte eindeutig bestimmt sind, dann sind es Symmetrieachsen von  Wobei ich nun ja wieder das Problem habe, dass ja die Symmetrieachsen keine Strecken, sondern Geraden sind, oder bin ich da jetzt ganz auf dem Holzweg???Hmm... --Goliath 18:24, 29. Apr. 2012 (CEST)
Wobei ich nun ja wieder das Problem habe, dass ja die Symmetrieachsen keine Strecken, sondern Geraden sind, oder bin ich da jetzt ganz auf dem Holzweg???Hmm... --Goliath 18:24, 29. Apr. 2012 (CEST)
Kommentar M.G.
Kreise existieren, egal ob wir sie im momentanen Interesse sind
@Wehnerj und natürlich für alle: "Wenn der Umkreis bestimmt wird ... " In der Mathematik geht es niemals darum, ob irgendeine Person irgendetwas macht ... . Der Mittelpunkt des Umkreises liegt auf der Hypotenuse egal ob der Umkreis bestimmt wird oder nicht.--*m.g.* 17:14, 29. Apr. 2012 (CEST)
Bestimmung von Geraden durch Strecken
@Goliath Zu je zwei verschiedenen Punkten existiert genau eine Gerade, die durch die beiden Punkte geht. Wir sprechen auch davon, dass die beiden Punkte die Gerade eindeutig bestimmen. Die beiden Punkte können auch die Endpunkte einer Strecke sein. Diagonalen sind Strecken. Dementsprechend ist durch eine Diagonale immer eine Gerade bestimmt. Anders ausgedrückt: Die Diagonalen eines Vierecks bestimmen immer zwei Geraden. Sie spezifizieren nun durch den bestimmten Artikel: Wenn die Diagonalen die Geraden bestimmen ... . Was ist mit den Geraden gemeint? Formulieren Sie am Besten noch mal ohne die Geraden zu verwenden indem sie die Diagonalen (Strecken) direkt als Symmetrieachsen verwenden. Dann ist das ganze nicht 100%ig korrekt weil Symmetrieachsen Geraden und nicht Strecken sind. Aber das bekommen Sie nach der nicht ganz korrekten Formulierung bestimmt repariert.--*m.g.* 17:28, 29. Apr. 2012 (CEST)
Zweiter Versuch von Goliath
@Goliath und natürlich auch für alle Interessierten:
"Wenn die Diagonalen einer Raute  durch die Strecken der Eckpunkte eindeutig bestimmt sind,... "
durch die Strecken der Eckpunkte eindeutig bestimmt sind,... "
Jede Strecke ist durch ihre Endpunkte eindeutig bestimmt. Wie auch immer, was ist wohl wichtiger: ob die Diagonalen durch zwei Streckenendpunkte bestimmt sind oder dass es sich um Diagonalen eines bestimmten Vierecks handelt? Bestimmt letzteres. Versuchen Sie es mal über die folgende Variante: Es sei  ein Viereck. Wenn
ein Viereck. Wenn  ..., dann sind die Geraden
..., dann sind die Geraden 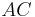 und
und 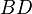 .... von ... .
.... von ... .
Versuchen Sie auch einfach mal abseits von jeder detailverliebten Genauigkeit zu formulieren was Sie prinzipiell ausdrücken wollen. Eigentlich doch folgendes: Wenn Viereck Raute, dann Diagonalen Symmetrieachsen. Was Sie eigentlich nicht wollen aber letztlich formulieren ist: Wenn Strecken Geraden bestimmen, dann sind Rauten achsensymmetrisch. (Hab versucht auf den Punkt zu bringen, hoffe es hilft. Nicht entmutigen lassen, Sie sind auf dem richtigen Weg.--*m.g.* 22:20, 29. Apr. 2012 (CEST)
@M.G. Erstmal vielen Dank für Ihre Mühe und die ausführliche Hilfestellung. Nein, lasse mich nicht entmutigen, jetzt bin ich motiviert, die Lösung hinzukriegen! Hab zumindest mal verstanden, was ich falsch gemacht habe! :-)
Also hier mein neuer Versuch:
Wenn  eine Raute ist, dann sind die Geraden
eine Raute ist, dann sind die Geraden 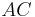 und
und 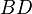 Symmetrieachsen von
Symmetrieachsen von  . --Goliath 23:13, 29. Apr. 2012 (CEST)
. --Goliath 23:13, 29. Apr. 2012 (CEST)
@Goliath So passt es! Merken Sie die Kraft der formalen Sprache der Mathematik? Die Dinge lassen sich letztlich einfacher und vor allem mit weniger Aufwand präzise ausdrücken. Die Diagonalen nennen wir einfach  und
und 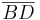 . Diese bestimmen eindeutig die Geraden
. Diese bestimmen eindeutig die Geraden 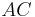 und
und 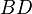 . Letztere sind Symmetrieachsen unserer Raute
. Letztere sind Symmetrieachsen unserer Raute  . Für die Schule müssen Sie es aber auch anders können. Probieren Sie es noch einmal mit mehr "normaler" deutscher Sprache.
. Für die Schule müssen Sie es aber auch anders können. Probieren Sie es noch einmal mit mehr "normaler" deutscher Sprache.
- Wenn ein Viereck eine Raute ist, dann sind ... .--*m.g.* 12:20, 30. Apr. 2012 (CEST)
@ M.G. Danke für die Tipps, so im Nachhinein ist es ja logisch!Naja, Übung macht den Meister! :-)Also dann, hier mein nächster Versuch:
Wenn ein Viereck eine Raute ist, dann sind deren Diagonalen Symmetrieachsen. (Oder müsste ich noch einfügen, dass es genau zwei Diagonalen sind???)--Goliath 16:06, 2. Mai 2012 (CEST)
@Goliath Nein, die Sache, dass es genau zwei Diagonalen sind, ist hier nicht das Problem. Wir kommen jetzt aber an den Punkt, an dem es relevant wird, dass die Diagonalen ja keine Symmetrieachsen sein können, weil sie ja nur Strecken und kleine Geraden sind. Für die Schule wäre Ihre Formulierung korrekt. Hier müssen wir dann etwas genauer werden: Wenn ein Viereck eine Raute ist, dann sind die Geraden, die durch .....--*m.g.* 17:14, 2. Mai 2012 (CEST)
@M.G.Danke für Ihre Geduld. Oh man, ich glaube ich stehe gerade voll auf dem Schlauch, aber ich probier es trotzdem nochmal: Also die Diagonalen sind Strecken von einen Eckpunkt zum gegenüberliegenden Eckpunkt des Vierecks. Bei der Raute verlaufen die Symmetrieachsen, welche Geraden sind durch diese Diagonalen hindurch. (Nur nochmal für mich vereinfacht, hoffe man kann das so sagen)Dann:
Wenn ein Viereck eine Raute ist, dann sind die Geraden, die durch die Diagonalen verlaufen Symmetrieachsen der Raute. (Mir ist jetzt kein anderes Wort als "verlaufen" eingefallen.)
Ich hoffe, ich bin jetzt nicht ganz am Ziel vorbei geschossen! --Goliath 17:52, 2. Mai 2012 (CEST)
Jetzt ist es völlig korrekt.--*m.g.* 23:05, 2. Mai 2012 (CEST)
@M.G. JUHU, jetzt hab ich es auch verstanden! --Goliath 14:46, 3. Mai 2012 (CEST)
Grundsätzliches
Eine mir vor allem auch für die Klausur wichtig erscheinende Frage ist, ob es Signal-Wörter gibt, die in eine Richtung der Implikation deuten. Gerade beim letzten Beispiel waren wir uns nicht ganz einig, ob "Wenn es ein Dreieck ist, dann beträgt die Winkelsumme 180°." oder "Wenn die Winkelsumme 180° beträgt, dann handelt es sich um ein Dreieck." die Implikation oder deren Umkehrung ist. Die Argumentationslinien sind einmal, dass man zuerst auf die Winkelsumme trifft (und in diesem Falle das Dreieck erst am Ende des Satzes genannt werden würde), andererseits dass das Dreieck das eigentlich Beherrschende des Satzes ist. Mir ist klar, dass es für die Aussage eigentlich unerheblich ist, da es sich um eine Äquivalenz handelt. Trotzdem fände ich es interessant, was denn jetzt die Umkehrung ist und was nicht. --Mathen00b 13:00, 3. Mai 2012 (CEST)

