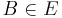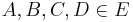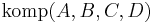Lösung von Aufgabe 6: Unterschied zwischen den Versionen
Aus Geometrie-Wiki
*m.g.* (Diskussion | Beiträge) (Die Seite wurde neu angelegt: Satz II: Je vier nicht komplanare Punkte sind paarweise verschieden. Formulieren Sie Teilaufgaben, die zu den Teilaufgaben a) bis f) von Aufgabe 4 analog sind und lös...) |
|||
| (3 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 4: | Zeile 4: | ||
Lösung: | Lösung: | ||
| + | # Satz II mit "wenn, dann" formulieren | ||
| + | # Satz II indirekt beweisen | ||
| + | # Kontraposition zu Satz II formulieren | ||
| + | # Kontraposition zu Satz II beweisen | ||
| + | # Umkehrung von Satz II formulieren | ||
| + | # Gilt die Umkehrung von Satz II? | ||
| + | |||
| + | <br /> | ||
| + | zu 1.<br /> | ||
| + | Es seien <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> vier Punkte. Wenn <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> nicht komplanar sind, dann sind sie paarweise verschieden.<br /> | ||
| + | <br /> | ||
| + | zu 2.<br /> | ||
| + | Voraussetzung: Es seien <math>A</math>, <math>B</math>, <math>C</math> und <math>D</math> vier Punkte mit <math>\operatorname{nkomp}(A,B,C,D)</math>.<br /> | ||
| + | Annahme: <math>A \equiv B</math> <br /> | ||
| + | |||
| + | |||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | Schritt || Begründung | ||
| + | |- | ||
| + | | 1) <math>\operatorname{nkomp}(A,B,C,D)</math> <br /> | ||
| + | 2) <math>\operatorname{nkoll}(A,C,D)</math> <br /> | ||
| + | 3) <math>A \equiv B</math> <br /> | ||
| + | 4) Es gibt genau eine Ebene <math>E</math>, die <math>A</math>, <math>C</math> und <math>D</math> enthält<br /> | ||
| + | 5) <math>B \in E</math> <br /> | ||
| + | 6) <math>A,B,C,D \in E</math><br /> | ||
| + | 7) <math>\operatorname{komp}(A,B,C,D)</math> <br /> | ||
| + | 8) (7) ist Widerspruch<br /> | ||
| + | 9) Annahme (3) ist falsch | ||
| + | ||1) Voraussetzung <br /> | ||
| + | 2) (1) (siehe Diskussion) <br /> | ||
| + | 3) Annahme <br /> | ||
| + | 4) Axiom I/4<br /> | ||
| + | 5) (3),(4) <br /> | ||
| + | 6) (4),(5) <br /> | ||
| + | 7) (6), Definition komplanar <br /> | ||
| + | 8) zur Voraussetzung (1) <br /> | ||
| + | 9) (8) | ||
| + | |||
| + | |}<br /> | ||
Aktuelle Version vom 3. Juni 2010, 18:34 Uhr
Satz II: Je vier nicht komplanare Punkte sind paarweise verschieden.
Formulieren Sie Teilaufgaben, die zu den Teilaufgaben a) bis f) von Aufgabe 4 analog sind und lösen Sie dann diese Teilaufgaben.
Lösung:
- Satz II mit "wenn, dann" formulieren
- Satz II indirekt beweisen
- Kontraposition zu Satz II formulieren
- Kontraposition zu Satz II beweisen
- Umkehrung von Satz II formulieren
- Gilt die Umkehrung von Satz II?
zu 1.
Es seien  ,
,  ,
,  und
und  vier Punkte. Wenn
vier Punkte. Wenn  ,
,  ,
,  und
und  nicht komplanar sind, dann sind sie paarweise verschieden.
nicht komplanar sind, dann sind sie paarweise verschieden.
zu 2.
Voraussetzung: Es seien  ,
,  ,
,  und
und  vier Punkte mit
vier Punkte mit 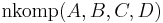 .
.
Annahme: 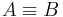
| Schritt | Begründung |
1) 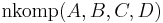 2) |
1) Voraussetzung 2) (1) (siehe Diskussion) |
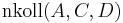
 , die
, die